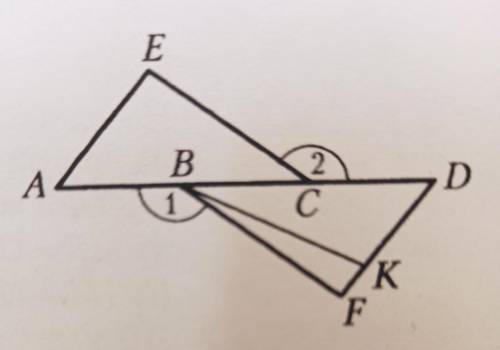
Угол А равен углу D, угол 1 равен углу 2, АВ=СD, ЕС = 10 см, угол АЕС равен 90 градусов. Найти высоту треугольника BKD, опущенную из вершины B.
Другие вопросы по теме Геометрия
Популярные вопросы
- 4предложения про футбольный клуб желательно на и ,...
2 - Для получения 25%ного раствора сахара к 6л воды добавили х кг сахара....
2 - Вгараже 25 машин.грузовых на 5 больше чем легковых.сколько в гараже грузовых...
2 - Какие из перечисленных обыкновенных дробей могут быть представлены в...
2 - Придумай свою или сказку 2 брата сформулировать и запиши главную мысль...
3 - Подчеркнуть подлежащее и сказуемое язык 1 класс лыжник идет по зимнему...
2 - Вкуске было 96 м ткани. для детского сада взяли 3/8 этого куска, а для...
2 - Подберите из орфографического словаря 10- 15 слов с приставками в-,без-,пере-.спишите...
2 - Эксковатр может выкопать за 1 час канаву длиной 20 метров .одну конаву...
3 - Почему говорят что глаза это зеркало души человека?...
3
Дано: ∠A=∠D, ∠1=∠2, AB = CD,
EC = 10 см, ∠AEC = 90°
Найти высоту ΔBKD, опущенную из вершины B.
ΔAEC и ΔBFD
1) ∠1 = ∠2 ⇒ ∠DBF = ∠ACE, как углы, смежные равным углам;
2) ∠A = ∠D — по условию;
3) AC = BD, т.к. AB=CD (по условию), BC — общая часть
Следовательно, ΔAEC = ΔBFD по равным сторонам и двум прилежащим к ним углам. ⇒
⇒ ∠BFD = ∠AEC = 90° ⇒
⇒ BF⊥ FD ⇒ BF ⊥ KD
Значит, BF — высота ΔBDK
Из равенства ΔAEC = ΔBFD ⇒ BF = EC = 10 см