1. Геометрия
  2. У равнобедренной трапеции

У равнобедренной трапеции диагональ 4см и с большой основой составляет 45 градусный угол. Найти среднюю линию трапеции. Найти площадь трапеции

mary357vozd80s mary357vozd80s    1   10.08.2022 13:33    1

Ответы
LeraBelenko LeraBelenko  10.08.2022 13:34

Средняя линия трапеции равна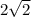 2\sqrt 2;

площадь трапеции равна 4

Объяснение:

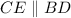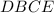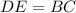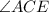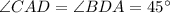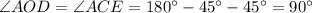Проведем CE\parallel BD. Тогда четырехугольник DBCE параллелограмм, DE = BC, \angle ACE — угол между диагоналями. Так как \angle CAD = \angle BDA = 45^\circ, то \angle AOD = \angle ACE = 180^\circ - 45^\circ - 45^\circ = 90^\circ.

В треугольнике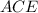 ACE по теореме Пифагора

AE = \sqrt {A{C^2} + C{E^2}} = \sqrt {{4^2} + {4^2}} = \sqrt {16 + 16} = \sqrt {32} = 4\sqrt 2 .

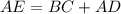Но AE = BC + AD, тогда средняя линия трапеции

\displaystyle\frac{{BC + AD}}{2} = \displaystyle\frac{{AE}}{2} = \displaystyle\frac{{4\sqrt 2 }}{2} = 2\sqrt 2 .

Найдем высоту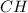 CH прямоугольного треугольника 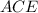ACE (она же и высота трапеции) по формуле

h = \displaystyle\frac{{ab}}{c} = \displaystyle\frac{{AC \cdot CE}}{{AE}} = \displaystyle\frac{{4 \cdot 4}}{{4\sqrt 2 }} = \displaystyle\frac{4}{{\sqrt 2 }} = \displaystyle\frac{{4\sqrt 2 }}{2} = 2\sqrt 2 .

{S_{ABCD}} = \displaystyle\frac{{AB + CD}}{2} \cdot CH = \displaystyle\frac{{AE}}{2} \cdot CH.

Значит

{S_{ABCD}} = \displaystyle\frac{{2\sqrt 2 }}{2} \cdot 2\sqrt 2 = 4.


У равнобедренной трапеции диагональ 4см и с большой основой составляет 45 градусный угол. Найти сред
ПОКАЗАТЬ ОТВЕТЫ
matveye234 matveye234  10.08.2022 13:34

Вообще  она решается в  одну  строчку ( см .  комменты  выше после условия  ) , но для полноты  решения  пришлось добавить ещё  две

Объяснение:


У равнобедренной трапеции диагональ 4см и с большой основой составляет 45 градусный угол. Найти сред
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Animerica20045 Animerica20045  24.12.2020 08:38
Ромбдун диагоналдары 8ди и жана 6 барабар анын жагын тап​...
Aidan23 Aidan23  24.12.2020 08:39
Площадь боковой поверхности первого цилиндра равна 28 см2. Чему равна площадь боковой поверхности второго цилиндра, если радиус основ данных цилиндров равен, а высота...
manukansona manukansona  24.12.2020 08:39
Две стороны прямоугольного треугольника равны:6 см и 9см. Найдите третью сторону треугольника. Рассмотрите все возможные случаи.​...
veraorfey veraorfey  24.12.2020 08:40
только там с решение надо это соч​...
kajaiuw kajaiuw  21.04.2019 14:34
Из вершины угла в треугольника авс проведён перпендикуляр вд к стороне ас. определите ас, если дс-ад=5, ав=21 и вс=24....
mila320 mila320  21.04.2019 14:26
Стороны параллелограмма доривнюе 6 дм и 10 дм одна из его диагонали 13 дм найдите другую диагональ параллелограмма​...
botan2008 botan2008  21.04.2019 14:22
Чему равен вписанный угол,который упирается на дугу, градусная мера которой равна 44°?...
wellbiss wellbiss  29.03.2021 20:42
Угол С равен 30 ДЕ равен 12 см Угол Д равен 60 Угол Найти СД в см​...
Mv0856 Mv0856  29.03.2021 20:41
Побудуйте ромб KPMT за стороною KP = 3 см і кутом К = 45° та по- верніть його на 60° навколо середини сторони КР за годинниковоюстрілкою.​...
Recor23 Recor23  25.09.2019 16:30
Треугольник вписан в окружность центр которой лежит на отрезке ав. найти градусные меры углов с и в если ∠а＝52º подробненько...

Популярные вопросы