У рівнобедреному трикутнику АВС основа АС=18см. Через середину висоти ВР, точку О, проходять промені АО і СО, які перетинають бічні
сторони в точках М і К. Знайдіть МК.
розписано будь ласка

Объяснение:

Проведем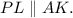 Так как 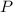— середина 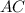, то 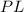— средняя линия треугольника 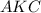, а т. 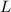— середина .

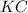Аналогично в треугольнике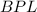 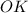проходит через середину стороны 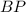параллельно основанию 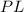, значит 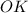— средняя линия и т. 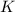— середина .

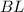Таким образом, точк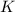и и 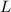разбивают сторону 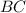на три равных отрезка.

Аналогичные рассуждения можно провести относительно другой боковой стороны треугольника.

Это значит, что треугольник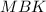и и 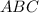подобны с коэффициентом

Тогда