У правильній чотирикутній призмі через середини двох суміжних сторін основи проходить площина, яка утворює з основою призми кут α і
перетинає три бічних ребра. Знайти площу перерізу, якщо сторона основи
призми А.
Другие вопросы по теме Геометрия
Популярные вопросы
- Перечитайте начало рассказа. Как автор знакомит читателя с котом? Паустовский....
1 - Как автор говорит об отношении девочки к своей деревушке? Какие слова выбирает?...
1 - Прочитайте описание кота. Подчеркните слова, которые для этого выбрал К.Г....
3 - Найдите в толковом словаре значение слова кратер или подберите синонимы. Кратер...
2 - В рассказе дано описание грозы. Впишите пропущенные слова. Дед с Ваней добрели...
1 - Перечитайте описания дождей. Какие признаки называет автор? Найдите эти слова...
2 - Составьте план рассказа. Запишите или нарисуйте. Расскажите кратко. Паустовский....
1 - Перечитайте строфу. Подчеркните устаревшие слова Жуковский. Вечер. Как слит...
2 - Вспомните, как называют писателя, который пишет басни....
1 - Допишите предложение. Былина...
3
Площадь сечения равна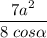 .
.
Объяснение:
В правильной четырехугольной призме через середины двух смежных сторон основания проходит плоскость, которая образует с основанием призмы угол α и пересекает три боковых ребра. Найти площадь сечения, если сторона основания призмы А.
Построим сечение.
В основании правильной призмы лежит квадрат.Отметим середины сторон АВ и AD и поставим точки К и Е соответственно. Соединим их.
Проведем диагонали АС и BD.
КЕ ∩ АС = Н.
Построим угол с вершиной в точке Н, равный α.
НР ∩ СС₁ = М.
Строим сечение, проходящее через три точки.
Продлим КЕ до пересечения с СВ и CD и поставим точки S и N соответственно.
S ∈ BB₁C₁C; M ∈ BB₁C₁C ⇒ S и M соединяем;
SM ∩ BB₁ = X;
N ∈ DD₁C₁C; M ∈ DD₁C₁C ⇒ N и M соединяем;
NM ∩ DD₁ = T;
X ∈ AA₁B₁B; K ∈ AA₁B₁B ⇒ X и K соединяем;
T ∈ AA₁D₁D; E ∈ AA₁D₁D ⇒ T и E соединяем;
EKXMT - искомое сечение.
Сечение представляет пятиугольник, состоящий из трапеции ЕКХТ и треугольника ХМТ.
⇒ S( EKXMT) = S(ЕКХТ) + S(ХМТ)
1. Рассмотрим ΔABD - прямоугольный.
AD = AB = a (условие)
По теореме Пифагора найдем BD:
BD² = AD² + AB² = 2a²
BD = a√2
ЕК - средняя линия ΔАВD.
Средняя линия равна половине длины стороны, которую она не пересекает.⇒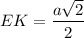 - меньшее основание ЕКХТ.
- меньшее основание ЕКХТ.
2. Рассмотрим ΔНРО - прямоугольный.
∠РНО = α (условие).
Диагонали квадрата равны и точкой пересечения делятся пополам.⇒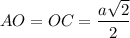
Средняя линия треугольника делит пополам любой отрезок, соединяющий вершину треугольника с какой-либо точкой основания.⇒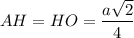
Косинус угла - отношение прилежащего катета к гипотенузе.ХТ = BD = a√2 - большее основание ЕКХТ.
3. Найдем площадь трапеции.
Площадь трапеции равна произведению полусуммы оснований на высоту.4. Рассмотрим ΔНМС - прямоугольный.
НС = НО + ОС
Тогда РМ = НМ - НР
5. Найдем площадь ΔХМТ.
Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.6. Теперь можем найти площадь сечения:
Площадь сечения равна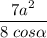 .
.
#SPJ1
MN - средняя линия BAD
Средняя линия отсекает треугольник, подобный исходному с коэффициентом 1/2.
Площадь MAN равна 1/4 площади BAD и 1/8 площади ABCD.
Тогда площадь MBCDN равна 7/8 площади ABCD.
S MBCDN = 7/8 a^2
Прямая призма, боковые ребра перпендикулярны основанию.
MBCDN является проекцией сечения MEFGN на плоскость основания.
Угол между плоскостью сечения и основанием равен α, отношение проекции к фигуре равно cosα.
S MEFGN = S MBCDN /cosα = 7/8 a^2 /cosα