1. Геометрия
  2. Три вершины трапеции находятся

Три вершины трапеции находятся в точках А(3; -1; 2), В(1; 2; -1) и С(-1; 1; -3). Найти уравнение средней линии трапеции, параллельной АВ.

Supreme222 Supreme222    1   09.11.2020 06:38    14

Ответы
6472krenko1 6472krenko1  09.12.2020 06:43

Дано:

Вершины трапеции

А(3; -1; 2), В(1; 2; -1) и С(-1; 1; -3)

МК - средняя линия

Найти:

Уравнение средней линии МК

Составим уравнение прямой АВ

\dfrac{x - x_A}{x_B - x_A} = \dfrac{y - y_A}{y_B - y_A} = \dfrac{z - z_A}{z_B - z_A}

\dfrac{x - 3}{1 - 3} = \dfrac{y +1}{2+1} = \dfrac{z - z_A}{-1 - 2}

\dfrac{x - 3}{ - 2} = \dfrac{y +1}{3} = \dfrac{z - z_A}{-3}

Таким образом, направляющий вектор прямой АВ

\overline p(-2;3;-3)

Проекции боковой стороны ВС на координатные оси равны

BC_x = x_C - x_B = -1 - 1 = -2

BC_y = y_C - y_B = 1 - 2 = -1

BC_z = z_C - z_B = -3 + 1 = -2

Найдём координаты точки К, принадлежащей боковой стороне ВС трапеции и, одновременно, средней линии.

x_K = x_B + 0.5BC_x = 1 + 0.5 \cdot (-2) = 0

y_K = y_B + 0.5BC_y = 2 + 0.5 \cdot (-1) = 1.5

z_K = z_B + 0.5BC_z = -1 + 0.5 \cdot (-2) = -2

Уравнение прямой МК, параллельной прямой АВ, то есть имеющей направляющий вектор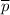 \overline p и проходящей через точку К

\dfrac{x - x_K}{p_x} = \dfrac{y - y_K}{p_y} = \dfrac{z - z_K}{p_z}

\dfrac{x }{-2} = \dfrac{y - 1.5}{3} = \dfrac{z+2}{-3}

Уравнение средней линии трапеции

\dfrac{x }{-2} = \dfrac{y - 1.5}{3} = \dfrac{z+2}{-3}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
verysadsavant1 verysadsavant1  18.08.2019 18:50
Найдите сторону ромба, площадь которого равна 12 квадратных сантиметров...
Maryna03 Maryna03  18.08.2019 18:50
Периметр ромба равен 20 сантиметров одна из его диагоналей равна 6 сантиметров найдите вторую диагональ ромба и площадь...
marfa228 marfa228  18.08.2019 18:50
На оснавании ac равнобедренного треугольника abc отмечены точки p и q та,что ap=cq.докажите, что треугольник pbq равнобедренный...
Лера100223 Лера100223  16.03.2021 18:49
9. Из точек А и В, лежащие в двух перпендикулярных плоскостях, проведены перпендикуляры АА1 и ВВ1 к прямой пересечения плоскостей. Найдите длину отрезка АВ, если АА1 = 21 см,...
koshtalev koshtalev  16.03.2021 18:49
MN||AB . найдите угол В, угол С и угол АСЕ ....
alehanagaitsewa alehanagaitsewa  16.03.2021 18:49
с контрольной .Геометрия 10 класс...
AveMartells AveMartells  16.03.2021 18:48
10 интересных фактов о именно населении северной Америки​...
Sn9 Sn9  16.03.2021 18:48
В равнобедренном треугольнике АВС, с основанием АС проведена биссектриса AD, ∠ С=72°. а) Докажите, что треугольник AСD равнобедренный; б) Сравните отрезки AC и BD. P/S нужно...
Varvarrrrrrrrrra Varvarrrrrrrrrra  16.03.2021 18:47
Комектесиндерши геометрия ​...
Kunpaw Kunpaw  10.09.2019 19:10
Ребро правильного тетраэдра равно корню 6 . найдите радиус шара вписанный в данный тетраэдр...

Популярные вопросы