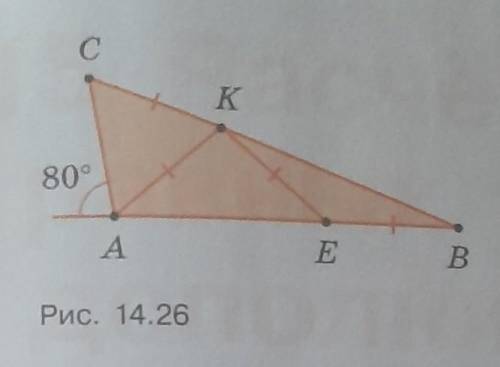
Треугольник с внешним углом, равным 80°, разрезали на три равнобедренных треугольника (рис. 14.25). Найдите меньший угол этого треугольника.
Другие вопросы по теме Геометрия
Популярные вопросы
- Поставьте знаки препинания в предложениях с однородными и неоднородными...
1 - Insonlar hayotida ham ahillik can dostlikning qudrati nimalarda korish...
2 - 2. на смесь меди и оксида меди (ii) массой 75 г подействовали избытком...
3 - Тыңда. қайтала. uқшіханзада ақ жейде, көк шалбар киеді. ол коныке...
1 - Как изменяются неметаллические свойства в направлении германии бром...
1 - получив на вход число x, ниже программа выводит два числа- m и n....
3 - Почему есть странные люди? инстаграм: khelthur...
2 - Количество книг на двух полках было одинаковое когда с первой полки...
2 - При каких натуральных значениях к дробь к-1/4 будетнужно...
3 - Болымсыздык және оздык есымдыктерын төмендегі сөздермен байланыстырып,...
2
////////////////////////////////////////////
20°
Объяснение:
Теорема о внешнем угле
<С+<В=80°
Пусть градусная мера угла <С будет у, а градусная мера угла <В будет х.
В равнобедренных треугольниках углы при основании равны.
<ЕКВ=<ЕВК.
<АЕК=<ЕКВ+<ЕВК теорема о внешнем угле треугольника.
<АЕК=2х
<КАЕ=<КЕА.
<КАЕ=2х.
Сумма смежных углов равна 180°
<САВ+80°=180°
<САВ=180°-80°=100°
Система уравнений
<С+<В=80°
<САК+<КАВ=100°
Составляем систему уравнений
{у+х=80° умножаем на (-1)
{у+2х=100°
{-у-х=-80
{у+2х=100
________ метод сложения
х=20°
Подставляем значение х в одно из уравнений
у+х=80°
у=80-20
у=60°
Угол <В=20° меньший угол в треугольнике