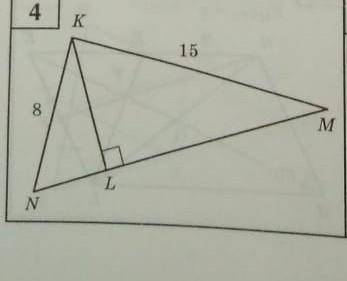
Треугольник NKM NK=8 KM=15 и высота KL​

Добрый день, ученик! Спасибо за твой вопрос. Давай разберемся вместе с этой задачей.

У нас есть треугольник NKM, где мы знаем, что сторона NK равна 8, а сторона KM равна 15. Также у нас есть высота треугольника KL, которую мы должны найти.

Для начала, давай вспомним основные определения. Высота треугольника - это линия, перпендикулярная к одной из сторон треугольника и проходящая через вершину, не лежащую на этой стороне. В данном случае, высота KL треугольника NKM будет проходить через вершину K и быть перпендикулярной к стороне NK.

Теперь, для того чтобы найти высоту KL, нам понадобится применить формулу для площади треугольника. Формула для площади треугольника звучит так: S = (основание * высота) / 2.

Но у нас есть одна проблема - мы не знаем длину основания, то есть стороны NK. Однако, у нас есть другая формула для площади треугольника, которую мы можем использовать. Это формула Герона. Она звучит так:

S = √(p * (p - a) * (p - b) * (p - c)),

где а, b и c - это стороны треугольника, а р - полупериметр треугольника, который можно найти как сумму всех сторон треугольника, деленную на 2. В нашем случае, a = NK, b = KM и c это сторона треугольника, которую мы должны найти - KL.

Таким образом, нам нужно найти площадь треугольника NKM, чтобы использовать формулу Герона. Воспользуемся формулой S = (основание * высота) / 2, где основание это сторона NK, а высота это KL.

Мы знаем, что площадь треугольника равна 60, так как данный ответ предоставлен нами по условию задачи.

Тогда, подставим известные значения в формулу и получим:

60 = (8 * KL) / 2,

120 = 8 * KL.

Теперь нам нужно найти KL, поэтому разделим обе стороны уравнения на 8:

120/8 = KL.

Если сделать эту операцию, то получим:

KL = 15.

Таким образом, найденная высота треугольника KL равна 15.

Надеюсь, что объяснение было понятным и полным. Если у тебя есть еще вопросы, не стесняйся задавать их!