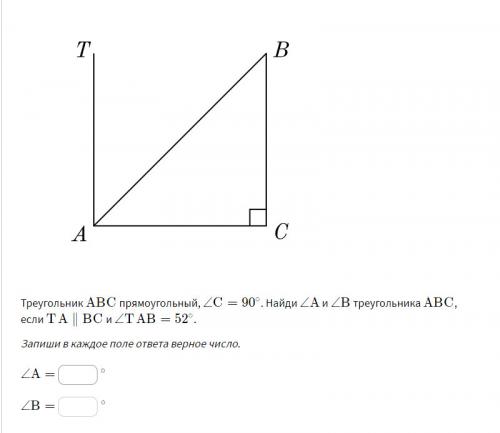
Треугольник ABCABC прямоугольный, \angle C=90^\circ∠C=90
∘
. Найди \angle A∠A и \angle B∠B треугольника ABCABC, если TA\parallel BCTA∥BC и \angle{TAB}=52^\circ∠TAB=52
∘
.
Другие вопросы по теме Геометрия
Популярные вопросы
- Протон начинает двигаться в области, где созданы однородные взаимно...
3 - Задание 4. Исследовали длину тела карася и получили следующие...
1 - Задание 1. Определение коэффициент корреляции между этими признаками....
3 - Частота света, соответствующая фотонам с энергией 50*10-19 Дж,...
1 - На рисунке изображен график производной функции f(x). Найдите...
3 - Знайдіть найбільше ціле число, що належить проміжку [5; 12).а)...
2 - «Процес» Ф. Кафки -які є можлив прочитання(інтерпретації) тобто...
1 - У якому рядку всі слова у словосполученнях вжито в прямому значенні?...
1 - Вкажіть, у якому рядку в усіх словах приголосні є дзвінкими....
2 - Позначте рядок, у якому всі слова пишуться за фонетичним принципом:...
2
TAB=52 circ<TAB=45 ответ значит будет angle A<A=50
Заметим, что углы TAB и CBT образуют внутренний фоновый угол при пересечении прямых TA и BC:
Фоновый угол TAB = Фоновый угол CBT = Тогда они равны между собой по свойству параллельных прямых
Также, в прямоугольном треугольнике ABC, сумма всех трех углов равна 180 градусам. Угол ABC прямой, поэтому у него мера равна 90 градусам.
Теперь мы можем найти меру угла A. Сумма углов TAB и BAT равна мере угла A:
Угол TAB + Угол BAT = Угол A
52° + 90° = Угол A
142° = Угол A
Затем, чтобы найти меру угла B, мы можем использовать сумму углов в угле треугольника.
Сумма углов в треугольнике ABC равна 180 градусам.
Угол A + Угол B + Угол C = 180°
142° + Угол B + 90° = 180°
Угол B + 232° = 180°
Угол B = 180° - 232°
Угол B = -52°
Но так как треугольник ABC является прямоугольным, углы должны быть положительными. Поэтому мы примем модуль от меры угла B:
Угол B = | -52° | = 52°
Итак, мера угла A равна 142 градусам, а мера угла B равна 52 градусам.