1. Геометрия
  2. Треугольник ABC - прямоугольник

Треугольник ABC - прямоугольник
AC = 10, AB=26, C=90°
найти CA,CH,Sabc

nastialeon nastialeon    3   26.12.2020 13:05    2

Ответы
Qw135tgv245 Qw135tgv245  25.01.2021 13:10

AC = 10

S_{ABC} = 120 квадратных единиц

Предположим, что CH - это высота треугольника проведенная из вершины прямого угла, тогда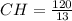 CH = \frac{120}{13}.

Объяснение:

Дано:

Δ ABC - прямоугольный, AC = 10, AB = 26, C = 90°.

Найти:  CA,CH,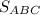 S_{ABC} - ?

Решение: По теореме Пифагора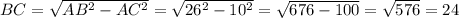 BC = \sqrt{AB^{2} -AC^{2} } =\sqrt{26^{2} -10^{2} }=\sqrt{676-100}=\sqrt{576}=24.

S_{ABC}=\frac{AC * CB}{2}=\frac{10 *24}{2} = 120 квадратных единиц. Предположим, что CH - это высота треугольника проведенная из вершины прямого угла.

Пусть AH = x, тогда BH = AB - AH = 26 - x.По тереме Пифагора:

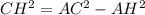
CH^{2} = AC^{2} - AH^{2}

                   ⇒ AC^{2} - AH ^{2} = BC^{2} - BH^{2}

CH^{2} = BC^{2} - BH^{2}

100 - x^{2} = 576 - (26 - x)^{2}

100 - x^{2} = 576 - 676 + 52x - x^{2}

200 = 52x |:52

x = \frac{200}{52}=\frac{50 * 4}{13 * 4} =\frac{50}{13}. По теореме Пифагора:

CH = \sqrt{AC^{2} -AH^{2} }=\sqrt{10^{2} -(\frac{50}{13} )^{2} } =\sqrt{100 - \frac{2500}{169} }=\sqrt{\frac{16900 - 2500}{169} }=\sqrt{\frac{14400}{169} }=\frac{120}{13}


Треугольник ABC - прямоугольник AC = 10, AB=26, C=90° найти CA,CH,Sabc
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
YaroslavShevchuk YaroslavShevchuk  15.04.2020 21:58
И ПОДРОБНО РЕШИТЬ ОЧЕНЬ НАДО ЛЮДИ :(...
GooodBaby GooodBaby  15.04.2020 21:58
Ребро куба ABCDA1B1C1D1 равно 12 см, точка М - середина ребра А1В1, точка N - середина ребра АА1. Найдите расстояние от точки А до плоскости D1MN....
Умникзаумник1 Умникзаумник1  15.04.2020 21:58
Знайдіть площу заштрихованої фігури за рисунком...
dimasikPro2 dimasikPro2  15.04.2020 21:58
Сравни длины отрезков, выходящих из вершины P, если ∡O=60°, ∡N=50°. Запиши отрезки в порядке возрастания их длин: Сравни длины отрезков, выходящих из вершины P, если...
Eldarval Eldarval  15.04.2020 21:58
До ть будь ласка! Знайти площу основи правильної чотирикутної призми, висота якої становить √ 2 см. Якщо її бічне √ 3 см...
Мурик123 Мурик123  15.04.2020 21:58
1.При переміщенні прямокутнийтрикутник ABC з катетами AC = 5 см іBC = 12 см перейшов у трикутникA B C . Знайдіть сторони трикутникаA B C . (26)​...
nikadey1 nikadey1  15.04.2020 21:58
В равнобедренном треугольнике ABC провели отрезок DE BC || DE(остальные данные на чертеже) 1.Рассмотрим длину страны DB ....
bobo6226 bobo6226  19.12.2019 15:09
Отрезки pq и st пересекаются в их общей середине. докажите, что прямые ps и tq параллельны....
ROLBER ROLBER  19.12.2019 15:09
1. периметр равнобедренного треугольника равен 7,3 м, а боковая сторона равна 2,1 м. найдите основание. 2. докажите равенство треугольников по двум сторонам и медиане,...
мамкакактус мамкакактус  19.12.2019 15:08
1. докажите что треугольник авс равнобедренный если у него высота bd является биссектрисой 2. отрезки равной длины ab и cd пресекаются в точке o так, что ао = od....

Популярные вопросы