Точки m и n середины сторон соответственно bc и cd параллелограмма abcd. отрезки am и bn пересекаются в точке о.найдите отношение mo/oa.
Другие вопросы по теме Геометрия
Популярные вопросы
- Длина и ширина прямоугольника вместе составляет 1 дм,при чём ширина равна 2 см....
3 - Зн. нули функции у = х (4) – 6х (2) – 7. в () это степинь....
2 - Сразделительного ь знак образуй новые слова от данных.гость -дерево.лист -пить.лиса...
1 - Если стрела выпущена из лука вертикально вверх из равномерно и прямолинейно движущегося...
3 - Підрахуйте і вкажіть кількість крові (в кг) в людини масою 55 кг. якщо відомо,...
2 - Дано натуральное число n. вычислить разницу между самой большой и самой маленькой...
3 - 34 за лучший 1. fill in the blanks with have got or has got . 1. alice a· nice...
3 - При каких значениях х, 5х-4 равно 30...
3 - Найди долю числа. напишите пример как делать подобные ! ? 1/4 от числа 24, 1/5...
3 - Кучу ! 1. дайте справку о соответствующем тексту направлении. какие черты этого...
3
BN ∩ AD = L
ΔBNC = ΔLND по стороне и двум углам прилежащим к ней (CN=DN по условию; ∠BNC=∠LND как вертикальные; ∠NCB=∠NDL как накрест лежащие), поэтому BC=LD.
Пусть BM = x, тогда BC = 2x.
LD=BC=AD ⇒ AL=2BC=4x
ΔMOB ~ ΔAOL по трём углам (∠MOB=∠AOL как вертикальные; ∠OBM=∠OLA и ∠OMB=∠OAL как накрест лежащие), поэтому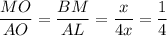
ответ: 1/4.