Точки M и N середины сторон AB и BC треугольника ABC. Найдите сторону AC, если MN = 4 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Кто знает как удалить аватарку в зум. У меня там нет такой функции(хочу удалить...
2 - Берілген тузуді берілген нүктеде жанайтын неше шеңбер жүргізуне болалы?...
2 - Чем должен руководствоваться ваш сверстник в общении с людьми пожилого возраста...
2 - У мужчины в детстве была удалена ретинобластома (опухоль глаза) - доминантный...
3 - Какая рифма у стихотворения Когда на меня навалилась беда???...
3 - Плес сделать проект на тему: Ситуативні вправи і задачі на анадіз явища інерції,...
3 - 1. Прийменником є виділене слово в реченніА Це вам не казочки про хмарки та...
2 - Решить задачи по экономике 1.Основное время на производство детали равно 30...
1 - Cоставьте картосхему природные зоны урала . Проведите границы природных зон...
3 - Спорофіт переважає в життєвому циклі.а) сфагнуму звичайного;б) плауна булавоподібногов)...
1
△ABC;
AM = MB;
BN = NC;
MN = 4 см.
Найти:АС = ? см.
Решение:Т.к. отрезок MN соединяет середины сторон треугольника АВС, то этот отрезок - средняя линия.
Исходя из этого, вспоминаем теорему средней линии: средняя линия треугольника параллельна основанию и равна его половине.
Поскольку отрезок MN параллелен основанию AC треугольника ABC и в 2 раза меньше этого основания, то АС = 4 * 2 = 8 см.
ответ: АС = 8 см.Дано:
△ABC; AM = MB; BN = NC; MN = 4
Найти:
АС = ?
Т.к. отрезок MN соединяет середины сторон треугольника АВС, то этот отрезок - средняя линия.
Поэтому по теореме средней линии: средняя линия треугольника параллельна основанию и равна его половине.
Значит, MN=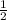 *AC, отсюда следует, что АС = 4 * 2 = 8 см.
*AC, отсюда следует, что АС = 4 * 2 = 8 см.
ответ: АС = 8 см.