1. Геометрия
  2. Точки k и n середины сторон

Точки k и n середины сторон cd и bc соответственно квадрата abcd со стороной а.найдите значение скалярного произведения: 1)ab*dc, 2)ad*cb, 3)bc*dc, 4)ac*dc, 5)ac*dc, 6)ac*cd, 7)ac*bd, 8) ak*an, 9)(ab+ad)(cd-cb)

ОляФомина ОляФомина    3   25.05.2019 19:20    3

Ответы
dianochkazhikh dianochkazhikh  01.10.2020 11:38

ответ дан Пользователем Emerald0101 Главный мозг

Исправлена опечатка в номере 8.


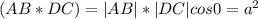
1) (AB*DC)=|AB|*|DC|cos0=a^2

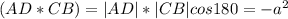
2) (AD*CB)=|AD|*|CB|cos180=-a^2

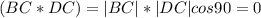
3)  (BC*DC)=|BC|*|DC|cos90=0

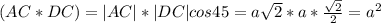
4=5) (AC*DC)=|AC|*|DC|cos45=a \sqrt{2}*a *\frac{ \sqrt{2} }{2}=a^2

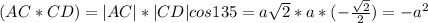
6) (AC*CD)=|AC|*|CD|cos135=a \sqrt{2}*a *(-\frac{ \sqrt{2} }{2})=-a^2

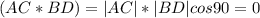
7) (AC*BD)=|AC|*|BD|cos90=0

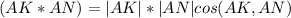
8) (AK*AN)=|AK|*|AN|cos(AK,AN)

AK= \sqrt{a^2+ \frac{a^2}{4} } = \frac{a \sqrt{5} }{2}

AN=AK=\frac{a \sqrt{5} }{2}

(AK,AN)=KAN=90-2*KAD

cos(AK,AN)=cosKAN=cos(90-2*KAD)=sin(2*KAD)=(BC*DC)=

=2sin(KAD)*cos(KAD)=2*\frac{KD}{AK}*\frac{AD}{AK}=2*\frac{2a}{2a\sqrt{5}}*\frac{2a}{a\sqrt{5}}= \frac{4}{5}

(AK*AN)= \frac{a \sqrt{5} }{2}* \frac{a \sqrt{5} }{2}* \frac{4}{5}= a^2.

9) AB + AD = AC; CD - CB = BD;

((AB+AD)*(CD-CB))=(AC*BD)=|AC|*|BD|cos90=0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Комарова23 Комарова23  13.04.2021 17:52
6. Унаслідок повороту навколо початку координат на 90° проти годинникової стрілки точка M(2; 0) переходить у деяку точку А. Знайдіть координати цієїточки.​...
Никита50005 Никита50005  13.04.2021 17:53
с заданием EDF = ? E = ? D = 131 градусов F = 90 градусов...
vorobeva85ramon vorobeva85ramon  13.04.2021 17:55
Два угла относятся как 4 к 7 а внешний угол третьего угла равен 121°. Найдите внутренние и внешние углы треугольника ​...
maks2614 maks2614  13.04.2021 17:56
в парке при музее решили разбить клумбу в форме четырёхугольника. Две стороны этой клумбы (AD и BC), если бы можно было продлить их на бесконечную длину, никогда б не пересеклись....
Малефисента7 Малефисента7  13.04.2021 17:56
Площади боковой и полной поверхностей правильной треугольной пирамиды соответственно равны 24√3 и 27√3 см². Найти сторону основания и высоту пирамиды.​...
Intagul Intagul  07.04.2020 17:23
Шостий член геометричної прогресії дорівнює 8,а знаменник дорівнює -4.Знайдіть сьомий член прогресії....
Оксана1970 Оксана1970  07.04.2020 17:23
Формула для нахождения площади круга, через длину. ​...
макар95 макар95  07.04.2020 17:22
За данным рисунка найдите площадь трапеции АВСD если ее средняя линия ранв...
Felissia12 Felissia12  07.04.2020 17:22
Большим диагональным сечением правильной шестиугольной пирамиды является равносторонний треугольник, сторона которого равна 30 мм. Вычисли объём пирамиды....
aksnov31526 aksnov31526  07.04.2020 17:22
На сторонах AB и BC треугольника ABC лежат точки M и N соответственно, угол A равен углу BMN равный 50 градусов, угол C равен 60 градусов. Найдите угол вас! Расспишите решение!...

Популярные вопросы