1. Геометрия
  2. Точки A и B лежат на сфере

Точки A и B лежат на сфере с центром O. Найдите радиус сферы, если AB=12√3 см, ∠AOB=120∘.

пончик123456798 пончик123456798    1   29.03.2021 09:25    1

Ответы
vladikn2016 vladikn2016  28.04.2021 09:27

R = 12 см.

Объяснение:

Дано: Точки A и B лежат на сфере с центром О, ∠AOB = 120°,

AB =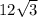 12\sqrt{3} см.

Найти: R - ?

Решение: AO = OB как радиусы сферы. Пусть AO = R, тогда OB = R.По теореме косинусов для треугольника ΔAOB:

AO^{2} + OB^{2} - 2AO *OB * cos ∠AOB = AB^{2}

R^{2} + R^{2} - 2 * R * R * cos(120) = (12\sqrt{3} )^{2}

2R^{2} + \frac{2R^{2} }{2} = 432

3R^{2} = 432 |:3

R^{2} = 144

R = 12 см.


Точки A и B лежат на сфере с центром O. Найдите радиус сферы, если AB=12√3 см, ∠AOB=120∘.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Mari2909 Mari2909  20.04.2021 21:02
1) кут КОА=70° , кут АОМ=19° 2)кут NOB=21° , кут KOB=111°​...
Sulifat Sulifat  20.04.2021 21:02
ОЧЕНЬ ВАЖНЫЙ ТЕСТ, А Я НИЧЕГО НЕ ПОНИМАЮ​...
Qocharian Qocharian  20.04.2021 21:03
1)Точки A(-1;-2; 4), B(-4;-2;0), C(3;-2;1) є вершинами трикутника. Зна- йдіть кут трикутника при вершині А2)Обчисліть площу паралелограма, побудованого на векторах а (8;4;1)і...
dima12345678909 dima12345678909  20.04.2021 21:05
На відрізку MN позначили дві точки D і C так, що MC:NC=7:5 і MD:ND=2:3. Знайдіть довжину відрізка CD, якщо MN=80 см....
Маришка945 Маришка945  20.04.2021 21:06
четырёхугольник ABCD описан около окружности и вписан в окружность прямые AB и CD пересекаются в точке M Найдите площадь четырехугольника если известно что угол AMD равен...
MiaDakota MiaDakota  20.04.2021 21:06
Знайти образ точки (1;0) при повороті навколо початку координат на кут 180 градусів проти годиникової стрілки...
Mas4323 Mas4323  30.03.2019 10:50
Втеугольнике abc угол a прямой ac=12см cosabc=0.6 найти вс...
adwa113eПомошник adwa113eПомошник  30.03.2019 09:39
Сделайте 2 и 3 нужно.отмечу как лучшим ☆☆☆​...
AliceКрошка AliceКрошка  30.03.2019 10:50
Втреугольнике abc, высота ad делит основание bc на отрезки. bd=2 корней из 3 см , dc=8 см, угол abc=60 градусов.найти ac...
AZINO7777 AZINO7777  30.03.2019 09:50
Втреугольнике abc ac=bc= 2 см, угол c равен 40. найдите высоту ah. дайте ответ в сантиметрах.​...

Популярные вопросы