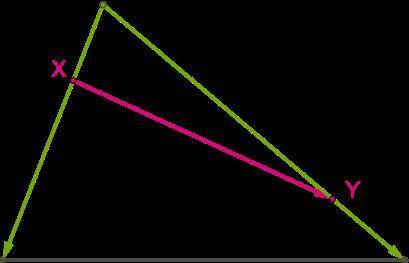
Точка X делит сторону DN в отношении DX:XN=2:1, точка Y делит сторону NK в отношении NY:YK=2:1.
Разложи вектор XY−→ по векторам ND−→− и NK−→−:
XY→=дробь⋅ND−→дробь⋅NK→.
Другие вопросы по теме Геометрия
Популярные вопросы
- Коли автомобиль проихав 0,3 а потим ще 0,4 усього шляху, то виявилося...
3 - Экономический фактор повлиявший на образование Великого шёлкового...
3 - Сумма частного чисел х и у и произведения чисел с и d...
2 - очень !! У трикутник ABC вписано ромб CDEF що кут C у них спільний...
3 - Упростите выражение: 1)ab+b²/3 : b³/3a + a+b/b 2)(a/a+4-a/a-4)×a+4/a...
1 - Dear Meg I m having a good time here in Bukhara. We are visit-ing...
2 - х1 и х2 - корни уравнения 2х^2 - 6х + q = 0. Найдите q, если х1^2...
2 - ТЕКСТ ЗАДАЧИ По наклонной плоскости поднимался груз массой 25 кг с...
2 - 5. Fылым мен техника жетістіктерін тарату мен оларды ел игілігіне...
1 - Какую чифпу следует поставить вместо* в числе8*243* что бы получимое...
1
В данном случае, отношения DX:XN=2:1 и NY:YK=2:1 дают нам информацию о разделении сторон на отрезки в данном соотношении.
Фактически, это означает, что точка X находится на отрезке DN так, что отрезок DX составляет 2/3 от общей длины DN, а отрезок XN составляет 1/3. Аналогично, точка Y находится на отрезке NK так, что отрезок NY составляет 2/3 от общей длины NK, а отрезок YK составляет 1/3.
Теперь давайте проведем разложение вектора XY→ по указанным векторам ND−→ и NK−→.
Обозначим вектор XY→ как a, вектор ND−→ как b и вектор NK−→ как c.
Тогда, по определению разложения вектора по векторам, мы можем записать:
a = x * b + y * c,
где x и y - скаляры (доли), определяющие разложение вектора a.
Теперь, чтобы определить x и y, мы можем использовать полученные нами отношения:
x = DX / DN = 2/3 и y = NY / NK = 2/3.
Теперь мы можем заменить эти значения в нашем уравнении:
a = (2/3) * b + (2/3) * c.
Таким образом, разложение вектора XY→ по векторам ND−→ и NK−→ составляет (2/3) * b + (2/3) * c.
Надеюсь, это решение ясно и понятно для вас. Если у вас есть еще вопросы, не сомневайтесь задавать их!