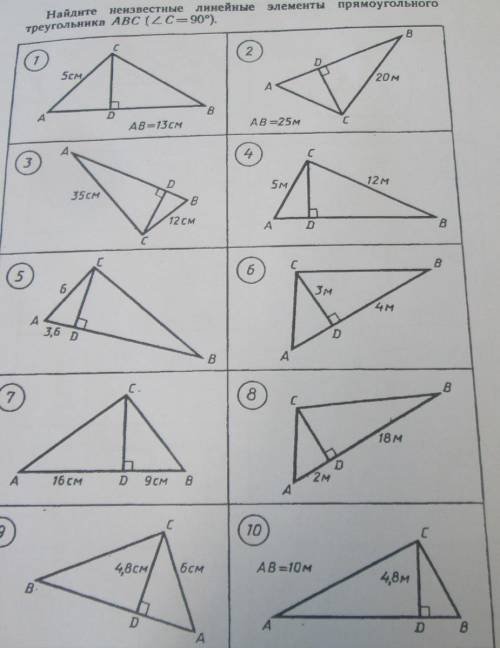
ТЕОРЕМА ПИФАГОРА. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ. Найдите неизвестные линейные элементы прямоугольного треугольника ABC (угол C =90) РЕШИТЕ 8 И 3

ТЕОРЕМА ПИФАГОРА. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ. Найдите неизвестные линейны

Ответы

gaviren 15.10.2020 16:03

Объяснение:

3) По теореме Пифагора

АВ²=АС²+СВ²

АВ²=35²+12²

АВ=√(1225+144)=√1369

АВ=37 см

Квадрат катета =произведению гипотенузы на проекцию этого катета

СВ²=АВ*DB

12²=37*DB

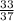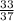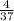
DB=144÷37=3 $\frac{33}{37}$ ,AD=37-3 $\frac{33}{37}$ =33 $\frac{4}{37}$

Квадрат высоты = произведению проекций этих катетов

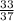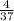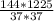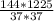CD²=DB*AD=3 $\frac{33}{37}$ *33 $\frac{4}{37}$ = $\frac{144*1225}{37*37}$ , CD=√( $\frac{144*1225}{37*37}$ )=12*35/37=420/37

8)AB=2+18=20 м

Квадрат высоты = произведению проекций этих катетов

CD²=AD*DB=2*18=36

CD=6 м

Квадрат катета =произведению гипотенузы на проекцию этого катета

AC²=AD*AB, АС=√(2*20)=2√10

По т. Пифагора

АВ²=АС²+АВ², СВ²=АВ²-АС²

СВ²=20²-(2√10)² , СВ=√(400-40)=√360=6√10

ПОКАЗАТЬ ОТВЕТЫ

vlad77r 26.01.2024 09:24

Для решения данной задачи нам потребуется использовать Теорему Пифагора.

Теорема Пифагора гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

В данном случае у нас имеется прямоугольный треугольник ABC, где сторона AC является гипотенузой, а стороны AB и BC - катетами.

В задаче дано значение одного катета, равного 8, и второго катета, равного 3. Наша задача - найти длину гипотенузы (стороны AC) и длину другого катета (стороны AB).

Давайте сначала найдем длину гипотенузы, используя Теорему Пифагора:

AC^2 = AB^2 + BC^2

В данном случае, AB = 8 и BC = 3, поэтому мы можем подставить эти значения в уравнение:

AC^2 = 8^2 + 3^2

AC^2 = 64 + 9

AC^2 = 73

Теперь найдем квадратный корень от обеих сторон уравнения, чтобы найти длину гипотенузы AC:

AC = sqrt(73)

AC ≈ 8.54 (округляем до двух десятичных знаков)

Таким образом, длина гипотенузы AC примерно равна 8.54.

Теперь найдем длину катета AB.

Для этого мы можем использовать Теорему Пифагора в другую сторону:

AB^2 = AC^2 - BC^2

Мы уже знаем значения AC, BC и AB^2 = 73, поэтому мы можем подставить их в уравнение:

73 = AB^2 - 3^2

73 = AB^2 - 9

AB^2 = 82

Теперь найдем квадратный корень от обеих сторон уравнения, чтобы найти длину катета AB:

AB = sqrt(82)

AB ≈ 9.06 (округляем до двух десятичных знаков)

Таким образом, длина катета AB примерно равна 9.06.

Итак, ответ на задачу:

Длина гипотенузы AC примерно равна 8.54, а длина катета AB примерно равна 9.06.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия