Таблица 9.1. Подобные треугольники
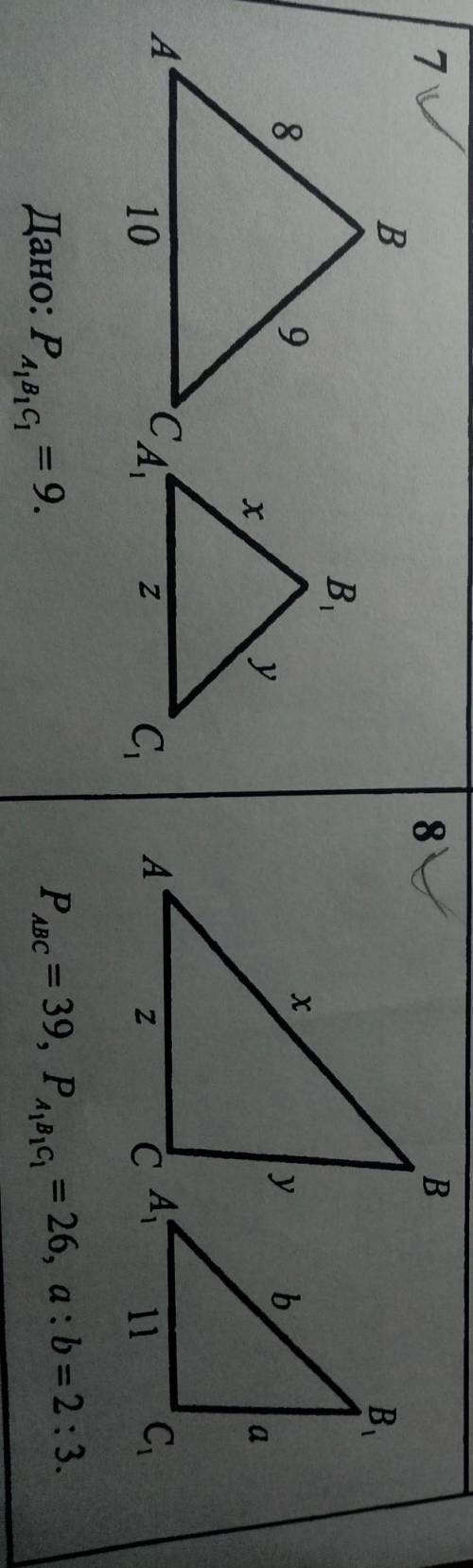
Дано:ABC ~ A1B1C1. Найти x, y, z
Другие вопросы по теме Геометрия
Популярные вопросы
- Reorder the words to make questions...
3 - Uyga vazifa. Hajm-oʻlchovni bildiruvchi so zlar ishtirokida 4-5 ta gap...
3 - Сторона паралелограма дорівнює 10 см, а висота, проведена до цеї сторони...
1 - На прямой обозначьте точки K, L, Ри Т. Сколько всего отрезполучилось? Запишите...
2 - Решить дифференциальное уравнение (см. фото)...
1 - Sin 6 a + sin 7 a - sin 8 a - sin 9 acos 6 a + cos 7 a + cos 8 a + cos...
2 - вычислить значения тригонометрических функций острых углов 30 и 60 градусов,...
2 - Поясни роль такої художньої деталі у творі, як портрет Фрідріхових дітей...
3 - Великий квадрат розділено на однакові маленькі квадратики. На якому із...
2 - До іть будь ласка скласти твір на тему: Мій улюблений літературний герой(за...
3
Подобные треугольники - это треугольники, у которых соответствующие углы равны, и их стороны пропорциональны.
Для решения этой задачи, нам нужно использовать соответствующие стороны треугольников ABC и A1B1C1.
Обозначим стороны треугольника ABC как a, b и c, а стороны треугольника A1B1C1 - a1, b1 и c1.
Используя соответствующие стороны, мы можем записать следующие пропорции:
a/a1 = b/b1 = c/c1
Из таблицы 9.1, видно, что:
a = y, a1 = 2y
c = 2z, c1 = z
b = x, b1 = 3x
Теперь мы можем записать пропорции:
y/2y = x/3x = 2z/z
Сократим каждую пропорцию:
1/2 = 1/3 = 2/1
Теперь мы можем найти значения x, y и z, решив каждую пропорцию по отдельности.
1/2 = x/3x
Умножим обе стороны на 3x:
3x * 1/2 = x
3x/2 = x
Умножим обе стороны на 2:
3x = 2x
Вычтем 2x из обеих сторон:
x = 0
Таким образом, получаем, что x = 0.
1/3 = y/2y
Умножим обе стороны на 2y:
2y * 1/3 = y
2y/3 = y
Умножим обе стороны на 3:
2y = 3y
Вычтем 3y из обеих сторон:
-y = 0
Умножим обе стороны на -1:
y = 0
Таким образом, получаем, что y = 0.
2/1 = 2z/z
Умножим обе стороны на z:
2z * 2/1 = 2z
4z/1 = 2z
Умножим обе стороны на 1/2:
4z = z
Вычтем z из обеих сторон:
3z = 0
Умножим обе стороны на 1/3:
z = 0
Таким образом, получаем, что z = 0.
В итоге, мы получаем, что x = 0, y = 0 и z = 0.