1. Геометрия
  2. Сума катетів прямокутного трикутника

Сума катетів прямокутного трикутника дорівнює 70 см, а сума медіани і висоти, проведеної до гіпотенузи, - 49 см. Знайдіть периметр
трикутника.

AripovZ AripovZ    3   26.08.2022 04:36    4

Ответы
jandar200 jandar200  26.08.2022 06:00

***

дано:

прямоугольный треугольник АСВ

CH - высота

СN - медиана

CH + CN = 79 см

АС+СВ=70 см

найти - периметр

медиана это отрезок который соединяет вершину треугольника с серединой противоположной стороны.медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.  m=\frac{1}{2} \cdot c где м - медиана, с - гипотенуза.

следовательно:

CN = \frac{1}{2} \cdot AB

высота это перпендикуляр, который опущен из вершины треугольника на противоположную сторону.св. синуса острого угла в прям. треугольнике  =>  h=\frac{ab}{c}  где а и b катеты прямоугольного треугольника, с - гипотенуза

следовательно:

CH = \frac{AC\cdot CB}{AB}

CH + CN = 79 см - по условию,

значит:

\frac{1}{2} \cdot AB + \frac{AC\cdot CB}{AB} = 49  

\frac{AB^2+2AC\cdot BC}{2AB} =49\\  

AB^2 +2\cdot AC\cdot BC= 98AB

по теореме Пифагора:

сумма квадратов длин катетов равна квадрату длины гипотенузы. c^2=a^2+b^2

следовательно:

AB^2 = AC^2 +CB^2

+

AC^2+CB^2 +2AC\cdot CB=98AB  

=>                                                                     << (a+b)^2=a^2+2ab+b^2>>

(AC+CB)^2=98AB\\

AC+CB=70\\

= \\

98AB=70^2

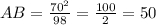
AB=\frac{70^2}{98} =\frac{100}{2} =50

периметр треугольника равен сумме длин всех его сторон. P=a+b+c,  где a, b, c - стороны

AB = 50

AC + CB = 70

=>

P= AC+CB+AB = 70+50=120

ответ: периметр треугольника равна 120 см.


Сума катетів прямокутного трикутника дорівнює 70 см, а сума медіани і висоти, проведеної до гіпотену
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
michael48 michael48  17.05.2019 22:30
Площадь круга на 55,04 дм меньше,чем площадь квадрата,описанного вокруг круга. найдите площадь круга...
прошу28 прошу28  17.05.2019 22:30
Около правильного треугольниу авс описала оружность,длина дуги ав равна 2π см. 1) найдите радиус окружности 2)длину одной из медиан треугольника авс...
teaonline teaonline  17.05.2019 22:30
Высота конуса 3√ 3см,образующая 6 см.найдите радиус описанного шара...
varfo varfo  29.05.2019 20:00
Площадь параллелограмма abcd со сторонами 5,4 равна 16. найдите длину его большей диагонали. ответ округлите до целого числа....
wwwvadimsokol wwwvadimsokol  30.11.2020 15:21
Известно, что m n. Замени знак * знаком сили или так, чтобы получить верное неравенство: — 0,4m * 0,4n....
хорошист536 хорошист536  30.11.2020 15:21
ABCD - параллелограммAB=5√3, AD =10 BAD =60°, AA1=12. Найти объем призмы ​...
Annalove2000 Annalove2000  30.11.2020 15:21
решите чему равен угол ТNM​...
нэла1 нэла1  23.04.2021 11:23
Більша діагональ прямокутної трапеції дорівнює 25 см, а висота - 7 см. Знайти площу трапеції, якщо її менша основа дорівнює 16 см Только с объяснением...
SlivkO0O154 SlivkO0O154  23.04.2021 11:24
Найти координаты вектора AB,если A(3;-4;1) B(-5;2-3)​...
He1111p He1111p  23.04.2021 11:24
запишіть рівняння кола, у яке переходить коло (x-2)2+(y-1)2=5 у результаті паралельного перенесення заданого вектором a(-1;1)...

Популярные вопросы