1. Геометрия
  2. Стороны треугольника 20см;

Стороны треугольника 20см; 34см; 42см. Найти радиус описанной и вписанной окружности.

HOUSEMAN222 HOUSEMAN222    2   18.04.2021 22:34    0

Ответы
аььарпашишки аььарпашишки  18.05.2021 23:35

Радиус описанной окружности (R) = 21,25 см, радиус вписанной окружности (r) = 7 см

Объяснение:

1) Найдём площадь треугольника за формулой Герона:

S =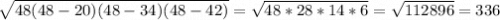 \sqrt{p(p-a)(p-b)(p-c)}, где p = \frac{a+b+c}{2}

p = \frac{20+34+42}{2} = 48 (см) — полупериметр

S = \sqrt{48(48-20)(48-34)(48-42)} = \sqrt{48*28*14*6} = \sqrt{112896} = 336 (см²)

2) Находим радиус описанной окружности.

Выразим из формулы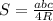 S = \frac{abc}{4R} неизвестное R

Получаем: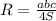 R = \frac{abc}{4S}

Подставляем числа в формулу и получаем:

R = \frac{20*34*42}{4*336} = \frac{28560}{1344} = 21,25 (см)

3) Находим радиус вписанной окружности.

Выразим из формулы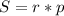 S = r * p неизвестное r (p — полупериметр = 48 см)

Получаем: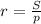 r = \frac{S}{p}

Подставляем числа в формулу и получаем:

Получаем: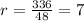 r = \frac{336}{48} = 7 (см)

ответ: R = 21,25 см, r = 7 см

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
vasapipkin934 vasapipkin934  05.04.2021 18:24
Решите задачу по геометрии 11 класс SOS...
Max1643 Max1643  05.04.2021 18:30
доведіть, що чотирикутник ABCD з вершинами в точках А(2; -2), В(1; 2), С(-3; 1) і D(-2; -3) є прямокутником​...
Мира2048 Мира2048  05.04.2021 18:33
569. На рис. 170 2 ВАС = 50°. Найдите угол ВОС.​...
ruslapanazavr ruslapanazavr  05.04.2021 18:33
Знайти косинус кута В трикутника ABC, якщо А (2; –4; 2), В (3; –3; 3), С (4; 0; 1)....
HiDolr HiDolr  05.04.2021 18:34
Я продолжаю свою историю от том как я решал тест не учась в школе...
alexguzz55 alexguzz55  02.02.2021 16:25
Решите 2 задачи по 2 рисункам...
0070070070007 0070070070007  02.02.2021 16:27
Основание равнобедренного треугольника равно 18см, а биссектриса делит боковую сторону на отрезки, из которых прилежащий к основанию равен 12мм.найдите периметр треугольника...
prostooo202003 prostooo202003  02.02.2021 16:31
Через точку E, лежащую вне окружности, проведены два луча,один из которых касается окружности в точке А, а другой пересекает окружность в точках В и С (рис. 19.4). AE = 12,...
Катя26031990 Катя26031990  13.09.2019 21:36
Точка a належить відрізку cd = 36см. знайдіть довжини відрізків ac і ad, якщо: 1) ac більший від ad на 4 см; 2) ac менший за ad у 2 рази; 3) різниця між ad і ac дорівнює...
Kaishuudee Kaishuudee  13.09.2019 21:29
Медиана прямоугольного треугольника, проведённая к гипотенузе, равна 20. из середины гипотенузы проведён перпендикуляр до пересечения с большим катетом. длина перпендикуляра...

Популярные вопросы