Средняя линия равнобедренной трапеции равна 8 см а диагональ 10 см найдите площадь трапеции​

Пусть дана равнобедренная трапеция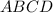 с диагоналя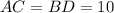ми см и 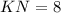см — медиана (см. вложение).

Сделаем дополнительное построение: проведем прямую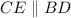 . Образовался равнобедренный треугольник 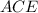с боковыми сторонами 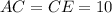см, равновеликий с трапецией 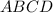(так как треугольник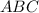и и 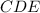равны по третьему признаку равенства треугольников). Следовательно, средние лини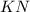и и 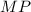тоже равны (средние лини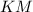и и 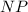соответственно равны треугольникам 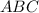и ).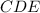

Рассмотрим равнобедренный треугольник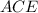 . Так как 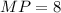см — его средняя линия, то 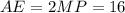см. Опустим перпендикуляр 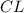— высота, биссектриса и медиана. Значит, 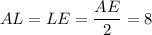см.

Рассмотрим прямоугольный треугольник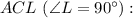

По теореме Пифагора: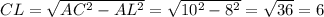 см.

Следовательно, площадь треугольника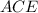 составляет 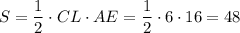см².

Так как треугольник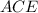 и трапеция 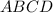равновеликие, то площадь трапеции равна 48 см².

ответ: 48 см².