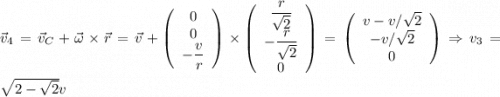19. Диск без проковзування котиться по горизонтальній поверхні. Швидкість центра диска о. Установіть відпо дність між модулями лінійних швидкостей точок на ободі диска відносно землі та відповідними точками рисунку с подробным решением файл с вопросами прикрепил

Другие вопросы по теме Физика
Популярные вопросы
- Контрольная по теме калужской области...
1 - Составьте фразу из букв. и с т е о н р о а н м о н е и е е...
2 - Ауданы 128см, ені ұзындығының 50%-ын құрайтын тіктөртбұрыштың ұзындығын...
3 - Под действием груза в 350 н пружина динамометра удлинилась на 0,4 см....
3 - Визначте троп для «вкраїна рідна» і «змучену, бідну». /виділені слова/...
1 - Сообщение на тему замени-надпиши ненужное...
1 - Твір опис про природу 10 речень...
3 - Составить текст i ve ever been...
2 - Прочитайте описание предмета или явления и назовите его, решив кроссворд....
2 - 1. у исполнителя омега две команды, которым присвоены номера: 1. прибавь...
3
Диск является твердым телом. Поэтому (по формуле Эйлера) скорость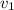 верхней точки
верхней точки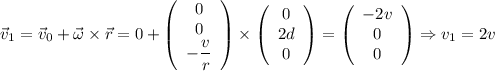 (здесь мы использовали, что нижняя точка -- является мгновенной осью вращения при движении без проскальзывания).
(здесь мы использовали, что нижняя точка -- является мгновенной осью вращения при движении без проскальзывания).
Скорость точки Г:
точки Г: 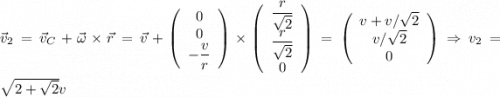
Скорость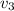 точки Б:
точки Б: 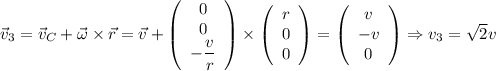 .
.
Скорость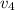 точки Д:
точки Д: