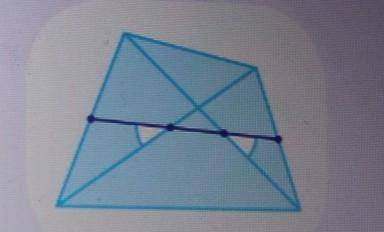
средняя линия четырехугольника образует с его диагоналями равные углы . докажите что диагонали этого четырехугольника равны ​

Для доказательства равенства диагоналей четырехугольника, у которого средняя линия образует с его диагоналями равные углы, будем использовать два треугольника, образованных диагоналями этого четырехугольника.

Пусть ABCD - данный четырехугольник, AF и CE - средние линии этого четырехугольника, пересекающиеся в точке O. Мы хотим доказать, что AO равна CO.

Для начала, давайте рассмотрим точку O и проведем через нее прямую OM, перпендикулярную AB. Обозначим точку пересечения этой прямой с диагональю BD как M.

Теперь, рассмотрим треугольники AOM и COM:

Треугольник AOM:
- AO - это половина диагонали AC, так как AF является средней линией и делит диагональ на две равные части.
- OM - это половина диагонали BM, так как OM перпендикулярна AB.
- Угол AOM равен углу AOC, так как средняя линия образует с диагоналями равные углы (по условию задачи).

Треугольник COM:
- CO - это половина диагонали BD, так как CE является средней линией и делит диагональ на две равные части.
- OM - это половина диагонали AM, так как OM перпендикулярна AB.
- Угол COM также равен углу COA, так как средняя линия образует с диагоналями равные углы.

Таким образом, у нас есть два треугольника AOM и COM, у которых совпадают:
- Сторона AO и CO, так как AO равна половине AC, а CO равна половине BD (по свойству средней линии).
- Сторона OM, так как OM перпендикулярна AB и делит диагонали на две равные части.

Таким образом, треугольники AOM и COM равны по двум сторонам и углу между ними, что означает, что они равны целиком. Это значит, что AO равно CO.

Таким образом, мы доказали, что диагонали AO и CO четырехугольника ABCD равны.