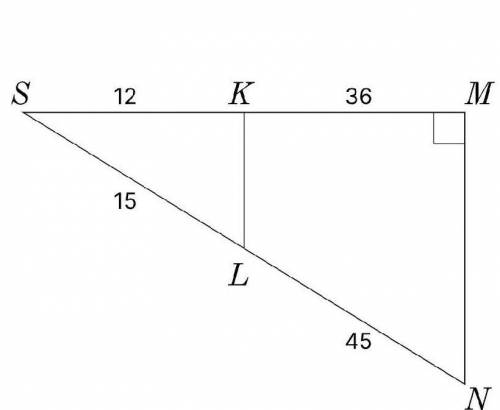
SK=12,KM=36,SL=15,LN=45,Kl=?

Для решения данной задачи, нам необходимо использовать свойства параллельных прямых и пропорциональности отрезков в подобных треугольниках. 1. Рассмотрим прямую KSN и прямую LNM. Они пересекают параллельные прямые SKM и SLN, поэтому углы KSN и LNM равны (как соответственные равные углы). 2. Также мы знаем, что треугольники KSN и LNM подобны, так как у них два угла исходного треугольника равны (они образованы двумя параллельными прямыми). 3. Следовательно, мы можем использовать свойство пропорциональности отрезков в подобных треугольниках. 4. В данной задаче, нам известны отрезки SK, KM и SL, для которых заданы значения: SK = 12, KM = 36, SL = 15. Нам нужно найти значение отрезка KL. 5. Мы можем написать пропорцию отрезков в подобных треугольниках в виде: SK : KL = SL : LN 6. Подставляя известные значения SK, SL и LN в пропорцию, получим: 12 : KL = 15 : 45 7. Теперь нам нужно решить эту пропорцию относительно неизвестного отрезка KL. Мы можем упростить эту пропорцию, деля числитель и знаменатель на их общий делитель. 4 : KL = 5 : 15 8. Затем мы можем умножить оба числителя и оба знаменателя на KL для получения пропорции без неизвестной переменной: 4 * 15 = 5 * KL 9. Выразив KL, получим: 60 = 5KL 10. Наконец, деля обе стороны на 5, получаем: KL = 12 Таким образом, мы нашли значение отрезка KL, оно равно 12.