Самостоятельная работа по теме свойства прямоугольного треугольника, 2 вариант

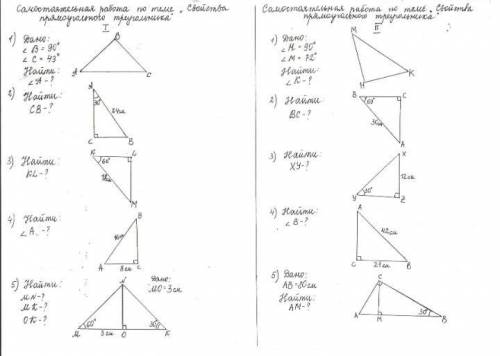
1. Решение: 90-72=18

В прямоугольном треугольнике угол можно найти: вычесть из 90 известный угол

ответ:18

2. AB в данном случае гипотенуза.

Угол А равен 30 градусов(90-60)

Свойство прямоугольного треугольника: катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.

Следовательно: BC в 2 раза меньше AB.

BC=AB÷2.

BC=30÷2=15

ответ:15

3. XY в данном случае гипотенуза( так как лежит напротив прямого угла).

XZ - катет, лежащий напротив угла в 30 градусов. По задаче помним свойство прямоугольного треугольника: катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.

Следовательно в обратную сторону: гипотенуза в два раза больше катета.

XY=2·XZ.

XY=2·12=24

ответ: 24

4. Видим, что AB - гипотенуза в 2 раза больше катета BC. Следовательно, уже известное нам свойство: катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.

Значит угол, лежащий напротив BC равен 30 градусов. ∠A=30°

Оставшийся угол, который нам нужно найти по задаче(∠B) найдем также, как и в первой задаче: в прямоугольном треугольнике угол можно найти: вычесть из 90 известный угол. Значит ∠B=90°-30°=60°

ответ: 60

5. CM в большом прямоугольном треугольнике ΔABC - высота. Данная высота образует другой прямоугольный треугольник ΔAMC.

В ΔABC известен ∠B=30°. Следовательно, оставшийся ∠A=90°-30°=60°

Также нам известна гипотенуза AB=80. Следовательно, по свойству напротив ∠B=30° лежит катет, который равен половине гипотенузы. Катет AC=80÷2=40

Рассмотрим ΔAMC:

∠A мы нашли, он равен 60°

∠AMC=90°(так как CM- высота)

∠ACM=90°-60°=30°(свойство из первого задания)

В ΔAMC AC будет гипотенузой, а AM - катет, лежащий напротив угла 30°. Помним то же самое свойство: катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.

Значит AM=AC÷2

AM=40÷2=20

ответ:20

Объяснение: