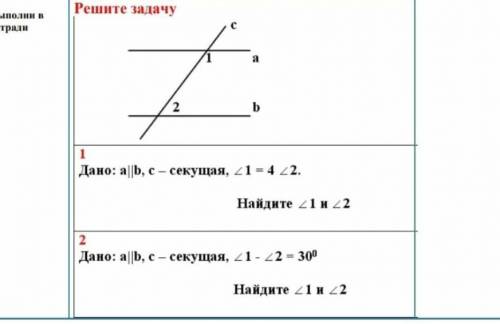
Решите задачу 1)Дано: a||b, c секущая, L1=4 L2.
Найдите L1 и L2
2)Дано: a||b, c- секущая, L1-L2 - 30⁰
Найдите 1 и 2​

Для решения задачи, нам потребуется использовать основные свойства параллельных прямых и перпендикуляров.

1) Задача: Дано a || b, c - секущая, L1 = 4, L2. Найдите L1 и L2.

Дано, что прямые a и b параллельны, а прямая c является их секущей (пересекает a и b). Также известно, что L1 = 4 и L2.

По свойству параллельных прямых, мы знаем, что когда секущая пересекает две параллельные прямые, у нас получаются соответственные углы (углы между a и c и между b и c) или вертикальные углы (углы расположенные напротив друг друга).

В данной задаче у нас даны соответственные углы (L1 и L2), значит они должны быть равны. То есть L1 = L2.

Таким образом, L1 = L2 = 4.

2) Задача: Дано a || b, c - секущая, L1 - L2 = 30⁰. Найдите L1 и L2.

Здесь также дано, что прямые a и b параллельны, а прямая c является их секущей. Но на этот раз известно, что разность между углами L1 и L2 равна 30⁰.

Мы также можем использовать свойство параллельных прямых, что соответственные углы равны. В данном случае, L1 - L2 = 30⁰ означает, что соответствующие углы имеют разность в 30⁰.

Поэтому, если мы обозначим один из углов, например, L1, то L2 будет составлять с ним угол величиной (L1 - 30⁰).

Таким образом, L1 - (L1 - 30⁰) = 30⁰.

Решим уравнение: L1 - L1 + 30⁰ = 30⁰.

30⁰ = 30⁰.

Значит, L1 может принимать любое значение. Однако, зная, что углы в треугольнике суммируются до 180⁰, мы можем сделать вывод, что L2 будет составлять с L1 угол величиной (180⁰ - L1 - 30⁰).

Таким образом, L1 и L2 могут быть любыми углами, при условии, что их сумма равна 180⁰ и L1 - L2 = 30⁰.

Надеюсь, что данное объяснение поможет вам понять, как решить данную задачу!