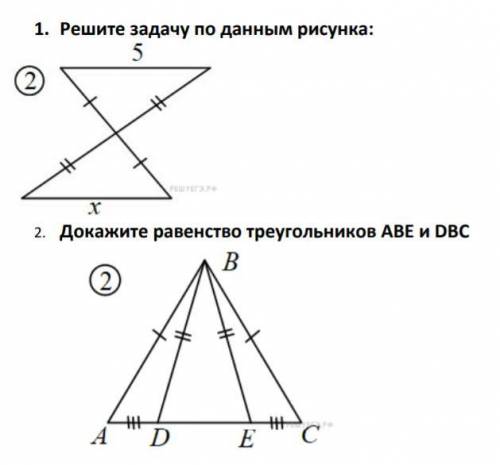
Решите 2 задачи.
даю 100б.
Другие вопросы по теме Геометрия
Популярные вопросы
- Из точки f, лежащей вне окружности, проведена касательная в точке е и...
3 - Впробирку добавляют несколько капель олеиновой кислоты и добавляют небольшое...
2 - Cd и ef - перпендикулярные прямые, угол aob=90 гр.,угол aof=125 гр.,найдите...
2 - 15 . нужно сочинить рассказ на тему мой день....
1 - Как происходит половое размножение у млекопитающих? описание....
1 - Как звали кота в сказке федорено горе?...
1 - Написать описание про мою лучшую подругу...
1 - 15 ! из формулы объема цилиндра v = π r² h выразите высоту h...
1 - Мусоргский картинки с выставки -что за произведение, почему так называется,...
3 - Гіпотенуза прямокутного трикутного трикутника дорінює 7 см, один з катетів...
3
1) Решение:
Рассмотрим 2 треугольника.
По рисунку видно, что у них 2 стороны соответственно равны,
так же равны углы между этими сторонами, т. к. они вертикальные
Тогда по 1 признаку треугольники равны => соответственные элементы равны. Тогда х = 5.
ответ: х = 5
2) Решение:
Рассмотрим треугольники ADB и CEB
AB = BC
AD = EC
DB = EB
Тогда по 3м сторонам (3й признак) эти треугольники равны, следовательно ∠С = ∠А
Рассмотрим треугольники ABE и DBC
AB = BC
AE = CD (т.к. AD = EC, а DE - общая)
док-во)
Тогда по 2м сторонам и углу между ними эти треугольники равны
ЧТД
∠1=∠2 (как вертикальные)
Треугольники равны по двум сторонам и углом между ними ⇒ x=5
№2△ABD=△CBE (по трём сторонам) ⇒ ∠ABD=∠CBE ⇒ ∠ABE=∠CBD
△ABE=△DBC (по двум сторонам (AB=BC, BE=BD) и углом между ними (∠ABE=∠CBD))