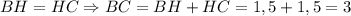Решить равнобедренном треугольнике авс боковая сторона равна корень из 3 ,а угол при основании равен 30 градусов.найти площадь и периметр треугольника
Другие вопросы по теме Геометрия
Популярные вопросы
- Втреугольникеabc ac =bc =13,ab =10 . найдите высотуch ....
3 - Дан прямоугольник abcd , периметр которого равен 14 см. сторонаab =...
3 - Втреугольникеabc ab =bc = 5 ,ac = 8 . найдите высотуbh ....
1 - Вместо машины определённой грузоподьемности для перевозки 45 т. груза...
1 - Вчисле 5349 мистер форд две цифры переставил местами, а потом одну цифру...
3 - Хождение в каноссу! расскажите кратко...
3 - Исправьте ошибки в предложении. в 661 все надо сделать?...
3 - Првиет) с переводом. 1. be patient 2. can i pick this? 3. tonight i...
1 - Втреугольникеabcab =bc =10 ,ac =12 . найдите высотуbh ....
3 - Какой мопед был у лёни из фильма любовь и голуби ?...
3
Объяснение:
Обозначим данный равнобедренный треугольник буквами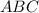 .
.
==========================================================
Проведём высоту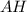 к основанию
к основанию 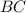 .
.
============================================================
Так как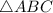 - равнобедренный
- равнобедренный 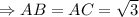 и
и 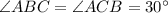 , по свойству.
, по свойству.
===========================================================
Рассмотрим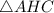 :
:
Если угол прямоугольного треугольника равен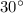 , то напротив лежащий катет равен половине гипотенузы.
, то напротив лежащий катет равен половине гипотенузы.
Найдём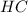 , по теореме Пифагора:
, по теореме Пифагора:
==========================================================
Так как