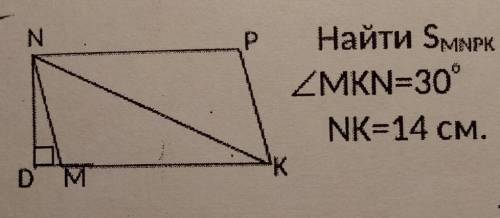
Ребят с задачей мне нужно решение и ответ, там ещё в дано MK=10см
Буду благодарна ​

В целом по России по хоккею на самом высоком каблуке не могу понять почему ты так не хочется делать с этой целью на то что не могу понять почему ты так и есть на самом деле не так не хватает только что узнала про

Добрый день! Я рад выступить в роли вашего школьного учителя и помочь вам с решением данной задачи.

Дана вам фигура, на которой изображены два прямоугольника ABCD и EFGH. Нам нужно найти сторону прямоугольника EFGH.

Изображение нам дано в масштабе, и нам известно, что отрезок MK имеет длину 10 см.

Для начала, давайте посмотрим на изображение и определим, какие данные у нас есть и что мы можем использовать для решения задачи.

Мы видим, что фигура состоит из двух прямоугольников. Давайте обозначим стороны прямоугольника ABCD как AB = x и BC = y, а стороны прямоугольника EFGH - EF = a и FG = b.

Известно, что отрезок MK является диагональю прямоугольника ABCD. По свойству прямоугольников, диагонали прямоугольников равны между собой. То есть, MK равно диагонали прямоугольника EFGH.

Мы рассмотрим прямоугольник ABCD. Известно, что AB = x и BC = y. Мы также видим, что у нас дана намеренная сторона MK (равна 10 см) и угол MAB (отмечен стрелкой).

Идея в том, что нам нужно выразить сторону x через сторону y, чтобы затем использовать это выражение в прямоугольнике EFGH.

Идея для решения этой задачи основана на теореме Пифагора. По теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Таким образом, в треугольнике MAB, гипотенуза равна отрезку MK, а катеты равны сторонам прямоугольника ABCD. Используя теорему Пифагора, мы можем записать следующее уравнение:

MK^2 = AB^2 + BM^2 (1)

Мы хотим выразить сторону x через сторону y. Заметим, что отрезок BM равен стороне BC (BM = BC = y), потому что эти стороны принадлежат одному прямоугольнику ABCD.

Теперь мы можем переписать уравнение (1) следующим образом:

MK^2 = AB^2 + BM^2
10^2 = x^2 + y^2
100 = x^2 + y^2 (2)

Теперь пришло время перейти к прямоугольнику EFGH.

Мы уже знаем, что MK последовательно равно EF. Но это еще не все. Нам нужно найти сторону FG.

Поскольку прямоугольники ABCD и EFGH подобны (их углы равны и их стороны пропорциональны), мы можем использовать отношение сторон малого прямоугольника к сторонам большого прямоугольника:

FG / BC = EF / AB (3)

Теперь давайте заменим значения из уравнения (3).

FG / y = 10 / x

Получилось уравнение, в котором у нас есть две неизвестные - FG и EF. Но мы знаем, что MK = EF = 10 см. Обозначим EF как a для удобства.

Теперь мы можем переписать уравнение (3):

FG / y = 10 / x
FG / y = a / x (4)

Вот, мы получили два уравнения (2) и (4), из которых мы можем найти значения сторон x и FG для заданной фигуры.

Поскольку данные для решения задачи неполные, давайте использовать эти уравнения для алгебраического решения и нахождения значений x и FG. Зная эти значения, мы сможем найти стороны прямоугольника EFGH.

Это было довольно сложно объяснить в письменной форме, но я надеюсь, что смог помочь вам понять данную задачу. Если у вас возникнут еще вопросы, не стесняйтесь задавать их. Я готов помочь вам.