Ребят
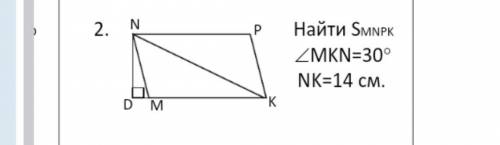
NM равно 8 см
нужно развёрнутое решение

Добрый день! Давайте разберемся с задачей. Из условия задачи видно, что отрезок NM равен 8 см. Нам нужно найти развёрнутое решение данной задачи. Для этого рассмотрим изображение. На изображении даны два треугольника - ABC и EDF. Нам известно, что отрезок NM является стороной треугольника EDF, а отрезок EF - стороной треугольника ABC. Чтобы найти развёрнутое решение, мы можем воспользоваться теоремой Пифагора. Эта теорема гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Обратите внимание на треугольник ABC. Сторона AB является гипотенузой, а стороны AC и BC являются катетами. То есть, мы можем записать следующее уравнение: AB^2 = AC^2 + BC^2 Так как треугольник ABC равнобедренный, то сторона AC равна стороне BC. Пусть это значение равно х. Тогда уравнение примет вид: AB^2 = x^2 + x^2 AB^2 = 2x^2 Теперь вспомним, что отрезок NM равен 8 см. То есть, AB + EF = 8. Заметим, что сторона EF является гипотенузой треугольника EDF, а сторона ED является катетом. Так как треугольник EDF прямоугольный, мы можем записать следующее: EF^2 = NM^2 - ED^2 EF^2 = 8^2 - x^2 EF^2 = 64 - x^2 Теперь мы можем установить связь между стороной AB и стороной EF. Мы знаем, что AB + EF = 8. Подставляя значения AB и EF из предыдущих уравнений, получаем: √(2x^2) + √(64 - x^2) = 8 Теперь мы можем решить это уравнение для определения значения x. Решение может быть сложным, поэтому рекомендуется использовать калькулятор или другие математические методы решения уравнений второй степени. Пошаговое решение можно предложить следующим образом: 1. Заменяем стороны AB и EF на выражения из уравнений выше: √(2x^2) + √(64 - x^2) = 8 2. Возводим оба выражения в квадрат, чтобы убрать корни: 2x^2 + 2√(2x^2)√(64 - x^2) + 64 - x^2 = 64 3. Упрощаем уравнение и переносим все члены в одну сторону: 2√(2x^2)√(64 - x^2) - x^2 = 0 4. Рассматриваем левую часть уравнения и упрощаем: 2√2x^3(64 - x^2) - x^2 = 0 5. Получаем уравнение: 2√2x^3(64 - x^2) = x^2 6. Разделяем нашу задачу на два уравнения: 2√2x^3 = x^2, где x ≠ 0 и 64 - x^2 = 0 7. Решаем первое уравнение: 2√2x^3 = x^2 Получаем x ≈ 5.472 8. Подставляем полученное значение x во второе уравнение: 64 - (5.472)^2 = 0 Получаем значение, отличное от нуля, что означает, что x не равно 0. Таким образом, мы нашли значение x и можем использовать его для определения длин других сторон треугольников ABC и EDF, а также для получения развернутого решения задачи. Надеюсь, эта подробная информация помогла вам понять, как решать данную задачу. Если у вас есть еще вопросы, не стесняйтесь обращаться за помощью!