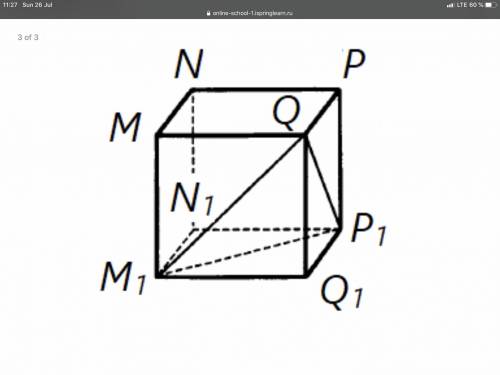
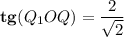Ребро куба MNPQM1N1P1Q1 равно 2. Найдите тангенс угла между плоскостями M1QP1 и M1N1P1.
Другие вопросы по теме Геометрия
Популярные вопросы
- Впр по окр мир. вариант 4. часть 1. запиши в строку ответа номера фотографий,на...
3 - 10 - 11 классыфранцузский язык5 mettez les verbes au futur simple au présent:...
2 - Наименьшая масса живого вещества характерны для природной зоны: а) арктические...
1 - Укажите название документа периода петра 1, в котором 1) все недвижимые вещи.....
1 - Втакси ,,люкс,, 16% всех машин иномарки. сколько всего машин в организации, если...
3 - Умишы 1000 рублей , а у маши столько же сколько и у сони. сколько рублей у маши...
1 - Определите величину заряда на который в поле с напряженностью 500 н/кл дейстаует...
2 - Расположите числа в порядке возрастания : -3 4/5; -7; 8/9; -11/13; 0...
1 - Какие районы рф отличаются наибольшей пестротой национального состава...
1 - Много 67. какой минирал искал герой сказов п.бажова данил-мастер у хозяйки медной...
1
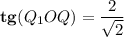
Объяснение:Обозначим середину диагонали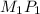 квадрата
квадрата 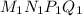 буквой
буквой 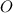 .
.
Угол между плоскостями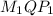 и
и 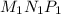 -
- 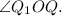
Так как у куба все ребра равны и ребро данного куба равно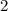 ⇒
⇒ 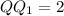
У квадрата все диагонали равны и делятся точкой пересечения пополам.
⇒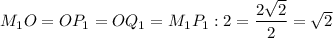
⇒