Равносторонний треугольник вписан в окружность, радиус которой равен 18 см. Найдите сторону треугольника. ​

Прежде всего замечаем, что радиус описанной окружности равен 2/3 высоты равностороннего треугольника. В свою очередь высота равностороннего треугольника:

h = a√3 / 2, где a - сторона треугольника, то есть

R = 2/3 · a√3 / 2 = a√3 / 3 ⇒ a = R√3 ⇒ a = 18√3 см

Примечание:

Так как задача на применение формулы - можно обойтись без чертежа.

18·√3 см

Объяснение:

По условию равносторонний треугольник ABC вписан в окружность, то в свою очередь окружность является описанной около треугольника ABC (см. рисунок).

Как известно, радиус R описанной окружности и сторона a равностороннего треугольника связаны формулой:

Отсюда: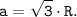

Так как радиус окружности известен R = 18 см, то можем найти сторону треугольника:

a = 18·√3 см.