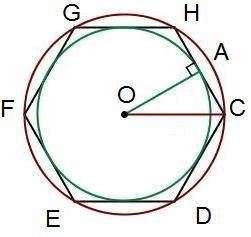
Радиус окружности, вписанной в правильный шестиугольник, равен 5 см. Вычисли сторону шестиугольника HC и его площадь.
HC=
5√3/3
10
5
5√ 3
10√ 3
10√3 /3 см
S=
10
50
25
50√ 3
25√ 3
10√ 3 см2
Другие вопросы по теме Геометрия
Популярные вопросы
- Put the verbs in the correct form. there (to be) 22 million homes...
2 - При каком значении с уравнение 3x^2+6x+c=0 имеет один корень !...
2 - Дискриминант квадратного уравнения 3x-1+6x^2=0?...
2 - Взоопарке живут 28 хищников.из них 8 тигров и 9 львов,а остальные-...
2 - Сочинение-рассуждение на тему почему человек который понапрасну теряет...
2 - Характеристика левши из сказа левша б-же не как у всех...
1 - Длины старон четырёхугольника 5 дм, 8 дм,9 дм,12 дм. найди его периметр...
3 - 27 в степени 2/3 минус (1/6) в /4 минус (√49 в 4 степени)^2 вычислить...
2 - Солнечные стали зажигать зайчик снежные узор на стекле . паж...
1 - √17. √12 в третей степени и √16^5 в 4 степени в виде степени...
2
Объяснение:
на фото, отметь как лучший
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
2. Все углы правильного шестиугольника равны между собой и равны 120 градусам.
Свойства окружности, вписанной в правильный шестиугольник:
1. Линия, проведенная от центра окружности до точки касания окружности со стороной шестиугольника, является радиусом окружности.
2. Радиус окружности, вписанной в правильный шестиугольник, равен половине длины стороны шестиугольника.
Теперь попробуем решить задачу.
1. Радиус окружности, вписанной в правильный шестиугольник, равен 5 см. По второму свойству окружности, радиус равен половине длины стороны шестиугольника. Поэтому длина стороны шестиугольника равна 2 * 5 см = 10 см.
Таким образом, ответ на первую часть вопроса "HC" равен 10 см.
2. Чтобы вычислить площадь шестиугольника, мы можем воспользоваться формулой для площади правильного шестиугольника:
S = (3 * √3 * a^2) / 2
где S - площадь шестиугольника, a - длина стороны.
Подставляем значение длины стороны a = 10 см в формулу:
S = (3 * √3 * (10 см)^2) / 2
Упрощаем выражение:
S = 3 * √3 * 100 см^2 / 2
S = 300√3 см^2 / 2
S = 150√3 см^2
Таким образом, ответ на вторую часть вопроса "S" равен 150√3 см^2.
В итоге, ответ на задачу:
HC = 10 см
S = 150√3 см^2.