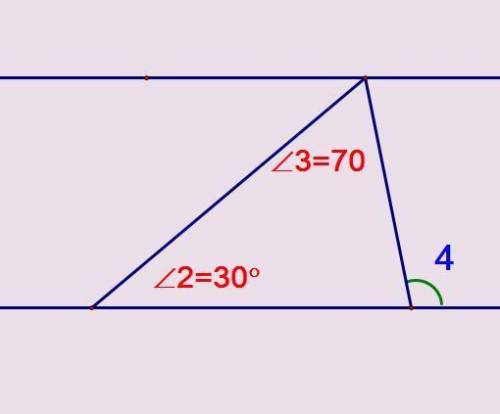
1.Медиана проведенная к основанию равнобедренного треугольника разбила угол при вершине этого треугольника на углы, равные 60 градусов. Найдите все углы треугольника. 2)Чему равен внешний угол треугольника изображенного на рисунке?
Другие вопросы по теме Геометрия
Популярные вопросы
- Одна сторона прям-ка равна 9дм.другая сторона 5дм. 6 см..найди периметр...
3 - Пожелтел орешник , и зарделись клены . обьясните почему перед и запятая...
2 - Хромосомы являются носителями наследственной информации так как в...
2 - Найти основу предложений в деревню сселили, а лозина все росла в чистом...
1 - А5. укажите, какое событие не относится к -японской войне 1) сражение...
2 - Значенье слов: свет, правда, истина....
2 - Токарь за 8 часов работы вытачивает 240 деталей, а его ученик за 6...
2 - Назовите достижения греческой культуры которые были положены в основу...
1 - Написать сочинение по картине зимнее утро игоря грабаря...
2 - Придумай заголовок и запиши его.придумай, что произошло потом, идопиши...
3
1. Для решения данной задачи мы можем воспользоваться свойствами медианы и углополовители в треугольнике.
Мы знаем, что медиана, проведенная к основанию равнобедренного треугольника, делит угол при вершине на две равные части. То есть, если угол при вершине треугольника равен 60 градусов, то каждая из частей этого угла будет равна 60/2 = 30 градусов.
Также, известно, что в равнобедренном треугольнике основания равны. Значит, каждый угол у основания треугольника будет равен (180-60-60)/2= 30 градусов.
Следовательно, все углы равнобедренного треугольника равны 30 градусов.
2. Чтобы найти внешний угол треугольника на рисунке, мы можем воспользоваться свойством суммы углов треугольника.
Сумма углов в треугольнике всегда равна 180 градусов.
На рисунке указаны два угла - 120 градусов и 50 градусов. Чтобы найти внешний угол треугольника, можно вычитать сумму из 180 градусов:
Внешний угол = 180 - (120 + 50) = 180 - 170 = 10 градусов.
Таким образом, внешний угол треугольника на данном рисунке равен 10 градусов.
Надеюсь, это объяснение помогло вам понять решение задачи! Если у вас еще остались вопросы, не стесняйтесь задавать.