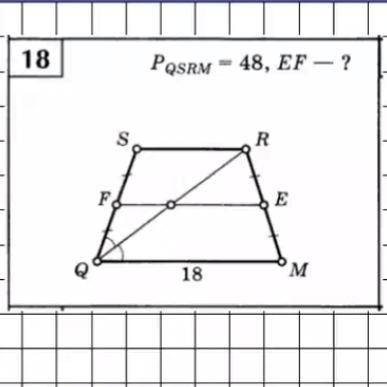
QRSM=равнобедренная трапеция
FE-средняя линия
QM=18
Pqrsm=48

Для начала, давайте поняжаем, что такое равнобедренная трапеция. Равнобедренная трапеция - это трапеция, у которой две стороны равны друг другу. В данном случае, трапеция QRSM является равнобедренной.

Также, в вопросе говорится, что FE - средняя линия трапеции. Средняя линия трапеции - это отрезок, соединяющий середины оснований трапеции. В данном случае, линия FE делит трапецию на две равные части.

У нас есть некоторая информация: QM = 18 и PQRS = 48. Мы должны найти значения других сторон и углов треугольников QFE и FEM.

Для решения этой задачи, мы можем использовать свойства равнобедренной трапеции. Одно из свойств гласит, что диагонали равнобедренной трапеции равны. Обозначим точку пересечения диагоналей как O.

Таким образом, мы можем сказать, что OE = EQ и OF = FQ. Кроме того, по свойству средней линии трапеции, мы знаем, что MF = FE.

Мы также можем заметить, что треугольники QFE и FEM - это равнобедренные треугольники, поскольку у них две стороны равны друг другу.

Теперь давайте решим задачу:

1. Поскольку QM = 18 и MF = FE, мы можем найти значение MQ, вычитая MF из QM: MQ = QM - MF = 18 - x (x - неизвестное значение MF).

2. По свойству равнобедренных треугольников, мы также можем сказать, что FM = MQ: FM = 18 - x.

3. Далее мы можем найти значение FO, вычитая OF из OM: FO = OM - OF = 48 - FM = 48 - (18 - x) = 30 + x.

4. Мы также знаем, что EO = EQ = x и FO = FQ = 30 + x, поскольку диагонали равнобедренной трапеции равны.

5. Используя теорему Пифагора в треугольнике QFE, мы можем написать следующее уравнение: x^2 + (18 - x)^2 = EQ^2.

6. Раскрываем скобки в этом уравнении и упрощаем его: x^2 + 324 - 36x + x^2 = x^2 + 36x + 900.
После упрощения, уравнение будет выглядеть так: x^2 - 72x + 576 = 0.

7. Решим это квадратное уравнение, используя метод факторизации или формулу корней. Предположим, что x_1 и x_2 - это корни этого уравнения.

8. Найдем эти корни и подставим их в уравнение, чтобы найти значения EO и FO.

9. Теперь, когда мы знаем значения EO и FO, мы можем найти длину EM, добавив EO и FO.

10. Наконец, используя свойство равнобедренных треугольников, мы можем найти значения углов QFE и FEM, так как у них две стороны равны.

Таким образом, мы можем найти все значение сторон и углов треугольников QFE и FEM, используя свойства равнобедренной трапеции и решение уравнения x^2 - 72x + 576 = 0.