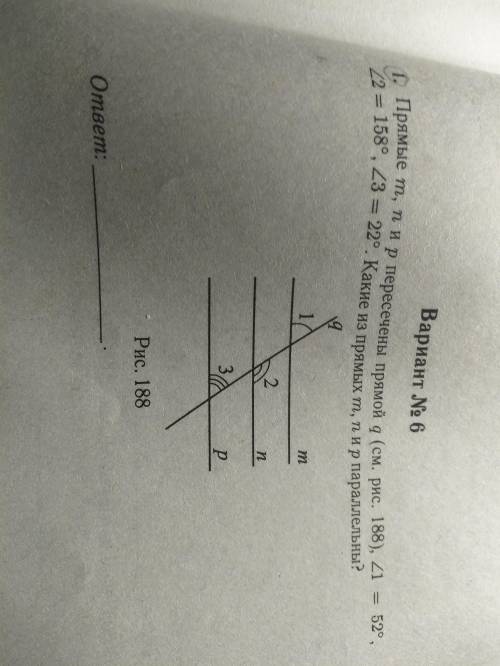
Прямые m, n, p пересечены прямой q, угол 1 = 2°,угол 2 = 158°, угол 3 = 22°. Какие из прямых m, n и p паралельны?

Чтобы определить, какие из прямых m, n и p параллельны, нам необходимо проанализировать значения углов и использовать свойство, что параллельные прямые имеют соответственные углы равными.

Давайте рассмотрим каждую пару прямых поочередно и посмотрим, какие из них параллельны.

1. Продолжим прямую m и прямую q до пересечения. Затем построим прямую, параллельную прямой q, проходящую через точку пересечения.


Теперь мы можем видеть два треугольника: треугольник, образованный прямыми m, q и новой прямой, а также треугольник, образованный новой прямой и прямыми q и p. Оба треугольника представляют собой треугольники, в которых два угла известны: 2° и 22°.

Учитывая свойство, что сумма углов треугольника равна 180°, мы можем найти третий угол в каждом треугольнике.
В треугольнике, образованном прямыми m, q и новой прямой: угол 1 = 180° - 2° - 22° = 156°.
В треугольнике, образованном новой прямой, q и p: угол 3 = 180° - 2° - 22° = 156°.

Мы видим, что угол 1 треугольника, образованного прямыми m, q и новой прямой, равен углу 2 треугольника, образованного новой прямой, q и p. Следовательно, прямая m || p.

2. Теперь рассмотрим прямые n и q. Продолжим прямую n до пересечения с прямой q. Затем построим прямую, параллельную прямой q, проходящую через точку пересечения.


Как и выше, мы имеем два треугольника: треугольник, образованный прямыми n, q и новой прямой, а также треугольник, образованный новой прямой, q и p. Оба треугольника имеют два известных угла: 158° и 22°.

Используя тот же принцип, что сумма углов треугольника равна 180°, мы можем найти третий угол в каждом треугольнике.
В треугольнике, образованном прямыми n, q и новой прямой: угол 1 = 180° - 158° - 22° = 0°.
В треугольнике, образованном новой прямой, q и p: угол 3 = 180° - 158° - 22° = 0°.

Угол 1 треугольника, образованного прямыми n, q и новой прямой, равен углу 2 треугольника, образованного новой прямой, q и p. Следовательно, прямая n || p.

Таким образом, мы можем сделать вывод, что прямые m и p параллельны, а также прямые n и p параллельны.