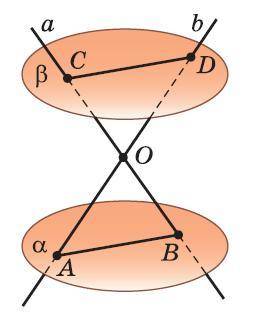
Прямые a и b, пересекающиеся в точке O, пересекают параллельные плоскости α и β соответственно в точках A, B и C, D. Найдите длину отрезка CO, если CB=31, CD=6, AB=2.
Другие вопросы по теме Геометрия
Популярные вопросы
- Что сближает повесть в.г. короленко в дурном обществе с рассказом л.н....
2 - Всем ! с решением. у=x³\3+x²-3x ( нужно исследовать функцию и построить...
2 - Используя из текста паустовского предложения с описанием осени напишите...
1 - петька на даче (в сокращении) озаглавьте первые 3 эпизода...
1 - Как найти площадь равнобедренного прямоугольного треугольника , если гипотенуза...
3 - Решите уравнение,: x+4=22x+7/x нужен только ответ...
2 - Как вода попдает на землю? она испаряется с неба в виде пара в виде подземных...
2 - 1he never stays in the hotels.2 i am reading a book from 5 to 7. 3 jake...
1 - Почему имущественное неравенство возникает в условиях производящего хозяйства?...
1 - Рассчитайте массу воды и массу соли которые необходимо взять для приготовления...
1
Согласно этой теореме, если прямая пересекает параллельные плоскости, то соответствующие отрезки, проведенные из точки пересечения до этих плоскостей, пропорциональны соответствующим отрезкам на одной плоскости.
Итак, мы знаем, что AB = 2, CB = 31 и CD = 6.
Мы хотим найти длину отрезка CO.
Для решения задачи мы можем использовать пропорцию отрезков на плоскостях α и β, базирующуюся на теореме Безузла.
Сначала найдем длину отрезка AO.
Мы видим, что отрезок CD представляет собой часть отрезка AO, поэтому мы можем написать пропорцию следующего вида:
AO/CO = CD/CB
Заменим значения по условию:
AO/CO = 6/31
Теперь мы можем выразить длину отрезка AO:
AO = CO * (6/31)
Теперь, чтобы найти длину отрезка CO, мы можем использовать пропорцию отрезков на плоскостях α и β снова:
CO/BO = CB/AB
Заменим значения:
CO/BO = 31/2
Теперь мы можем выразить отношение CO и BO:
CO/BO = 31/2
Мы также знаем, что BO = AO - AB. Заменим это в выражении:
CO/(AO - AB) = 31/2
Теперь мы можем выразить CO:
CO = (31/2)(AO - AB)
Мы уже знаем, что AO = CO * (6/31), поэтому мы можем заменить это в выражении:
CO = (31/2)(CO * (6/31) - AB)
Раскроем скобки:
CO = (31/2)(6/31 * CO - AB)
Сократим дроби и упростим:
CO = (6/2)(6 - AB)
Теперь заменим AB = 2 и решим выражение:
CO = (6/2)(6 - 2)
CO = (6/2)(4)
CO = 3 * 4
CO = 12
Таким образом, длина отрезка CO равна 12.