Прямая ом перпендикулярна к плоскости правильного треугольника abc и проходит через центр о этого треугольника, ом = а, ∠mco = φ. найдите: а) расстояние от точки м до каждой из вершин треугольника abc и до прямых ав, вс и сa; б) длину окружности, описанной около треугольника abc; в) площадь треугольника abc.

а)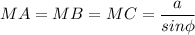

б)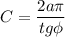

в)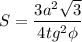

Объяснения:

Пусть К, Н и Р - середины сторон АВ, ВС и АС соответственно, тогда

АН⊥ВС, ВР⊥АС, СК⊥АВ (треугольник правильный, медианы, высоты и биссектрисы совпадают).

Центр О правильного треугольника АВС равноудален от вершин и от сторон треугольника, т.е.

АО = ВО = СО,  КО = НО = РО, а эти отрезки - проекции соответствующих наклонных на плоскость треугольника, значит

МА = МВ = МС - расстояния от точки М до вершин

и  МК = МН = МР - расстояния от точки М до сторон (МК⊥АВ, МН⊥ВС, МР⊥АС по теореме о трех перпендикулярах).

а) ΔМОС: ∠МОС = 90°,

___

____

, так как медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины.

Из прямоугольного треугольника МОК по теореме Пифагора:

___

____

б) СО - радиус описанной окружности. Тогда длина окружности:

_____

в)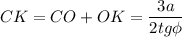

Площадь правильного треугольника АВС: