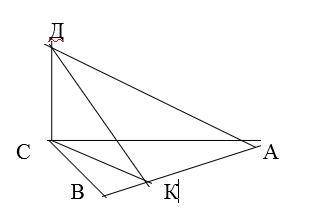
⦁ Прямая CD перпендикулярна к плоскости остроугольного треугольника ABC, у которого CK – высота . Найдите расстояние от точки A до плоскости CDK, если DA = 8 см, а DAK = 45градусов

Для решения данной задачи нам понадобится знание свойств перпендикулярных прямых и треугольников, а также некоторых геометрических формул.

Первым шагом определим, какая информация нам уже дана:
- У нас есть остроугольный треугольник ABC, в котором CK является высотой.
- Мы знаем, что прямая CD перпендикулярна к плоскости треугольника ABC.
- Длина отрезка DA составляет 8 см.
- Угол DAK равен 45 градусам.

Теперь возьмемся за решение задачи.

1. Нарисуем остроугольный треугольник ABC с высотой CK и точкой D на прямой CD. Также нарисуем плоскость CDK.

2. Обозначим точку пересечения плоскости CDK с высотой CK как точку E. Точка E будет находиться на прямой CD.

3. Из свойства перпендикулярных прямых следует, что угол EAK также равен 90 градусам, так как он образован пересечением прямой CD и плоскости CDK.

4. Заметим, что треугольник DAE является прямоугольным и прямоугольный треугольник DAE.

5. Так как угол DAK равен 45 градусам, то угол EAK также равен 45 градусам. Значит, треугольник DAE будет прямоугольным и равнобедренным.

6. Из равнобедренности треугольника DAE следует, что отрезок DE равен отрезку AE.

7. Имеем две равные стороны в треугольнике DAE: DA = 8 см и DE = AE.

8. Теперь воспользуемся теоремой Пифагора для нахождения третьей стороны треугольника DAE.

Теорема Пифагора гласит, что квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин двух других сторон.

В нашем случае гипотенуза — сторона DE, а катеты — сторона DA и сторона AE.

Запишем формулу теоремы Пифагора:
DE^2 = DA^2 + AE^2

9. Возьмем в качестве переменной длину отрезка AE и обозначим его как x.

Тогда формула теоремы Пифагора примет следующий вид:
DE^2 = 8^2 + x^2

10. Распишем формулу расстояния от точки A до плоскости CDK через отрезок AE:
Расстояние = AE

11. Используем равенство DE = AE, которое мы получили на шаге 6.

12. Берем уравнение (9), заменяем DE на AE:
x^2 = 64 + x^2

13. Сократим x^2 с обеих сторон уравнения:
0 = 64

Получили противоречие. Уравнение не имеет решения.

Ответ: расстояние от точки A до плоскости CDK не может быть найдено, так как уравнение не имеет решения.

Обоснование: Мы использовали свойства перпендикулярных прямых, равнобедренности треугольника DAE и теорему Пифагора для решения задачи. Однако, при решении уравнения, полученного из теоремы Пифагора, мы столкнулись с противоречием, что говорит о том, что задача имеет несовместное условие и не может быть решена.