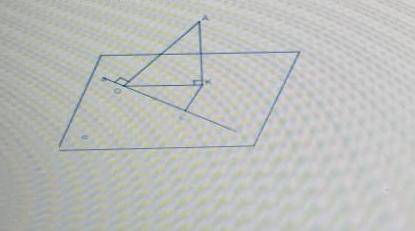
Прямая а лежит в плоскости альфа, Отрезок АО перпендикулярен прямой а, АК перпендикулярен плоскости альфа. Точка К лежит в плоскости альфа, точка L принадлежит прямой а. Найдите АК, если ОК=ОL, KL=2корень из 2, угол АОК=60градусов
Другие вопросы по теме Геометрия
Популярные вопросы
- Решить уравнения: (r-1908)-92=4630...
3 - Доклад на тему симфоническая музыка...
2 - Шукиршилик етемин осы омириме перевод...
2 - Биологическое процветания вида, преобладает рождаемости над смертности...
1 - Какие промышленные предприятия есть в томске...
3 - Число 1/9, 3/5, 3/2, 5/7 разделить; а) на 3; б) нач 1/3...
2 - 27. last weekend we enjoyed a city break in chester, the ancient medieval...
1 - Для кокого класса хордовых характерно наличие двойного дыхания...
1 - Нарисовать расшалившиеся буквы к и ю...
2 - Ваквариуме морского музея 444 моллюска .из них гребешков 5 раз больше...
3
Дано:
- прямая а лежит в плоскости альфа
- отрезок АО перпендикулярен прямой а
- точка К лежит в плоскости альфа
- точка L принадлежит прямой а
- ОК = ОL
- KL = 2корень из 2
- угол АОК = 60 градусов
Задача состоит в нахождении значения отрезка АК.
Решение:
1. Из условия задачи следует, что отрезок АО перпендикулярен прямой а. Это означает, что угол АОК прямой, то есть 90 градусов.
2. Также, из условия задачи, мы знаем, что ОК = ОL. Это означает, что точка K находится на середине отрезка ОL.
3. Мы можем разделить отрезок ОL напополам, чтобы найти точку K. Для этого, мы найдем половину длины отрезка ОL: KL/2.
4. Подставляем известные значения в формулу: KL/2 = 2корень из 2/2 = корень из 2.
5. Таким образом, отрезок АК равен найденной половине длины отрезка ОL, то есть АК = корень из 2.
Итак, ответ на задачу состоит в том, что АК = корень из 2.