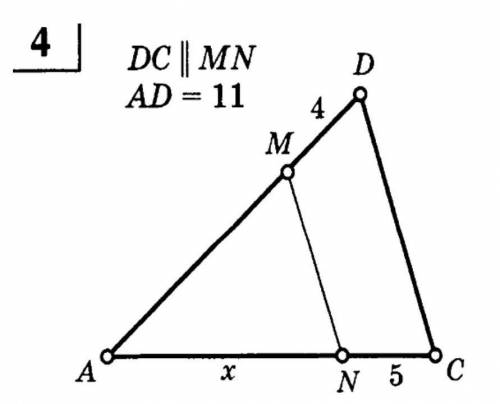
Геометрия 8 класс найти x, y​

Давайте решим эту задачу вместе.

На данной схеме у нас есть две пары параллельных прямых: AB || CD и AC || BD. Также нас интересуют две точки пересечения этих прямых, обозначенные как M и N. На схеме также видно, что угол BAC равен 110 градусам.

Наша задача - найти значения переменных x и y.

Для начала давайте посмотрим на треугольник ABC. У нас есть только один угол, равный 110 градусам. Мы знаем, что сумма углов треугольника равна 180 градусам, поэтому угол BAC + угол ABC + угол BCA = 180.

Давайте обозначим угол ABC как z. Тогда у нас будет уравнение:

110 + z + 90 = 180.

Суммируя углы и упрощая уравнение, мы получим:

z = 180 - 110 - 90.

Решим это уравнение:

z = 80 градусов.

Таким образом, мы нашли значение угла ABC - он равен 80 градусам.

Известно также, что $\ hoyCD=2x-30 $ и $\ hoyAB=x-20 $. Как вы заметили, отрезки CD и AB являются параллельными и имеют одну общую точку - точку M, а также угол ABC равен 80 градусам, поэтому мы можем использовать свойство параллельных прямых.

У нас есть две теоремы параллельных прямых, которые нам помогут в решении этой задачи.

1. Теорема об альтернированных углах:
Если две параллельные прямые пересекаются с третьей прямой, то каждая пара альтернированных углов равна.

2. Теорема об альтернированных углах (векторный вид):
Если две параллельные прямые пересекаются с двумя пересекающимися прямыми, то отношение длин отрезков между точками пересечения прямых равно отношению длин отрезков между точками на прямых.

Относительно точки M мы можем применить первую теорему и сказать, что:

уголMBC = угол（x-20）.

Угол MBC также является альтернированным углом для угла ABC, поэтому мы можем записать следующее уравнение:

ABC = MBC.

Так как ABC равно 80 градусам, мы можем записать:

x-20 = 80.

Решим это уравнение:

x = 80 + 20.

Таким образом, мы нашли значение переменной x - оно равно 100.

Теперь перейдем к переменной y. Нам известно, что точка N является точкой пересечения прямых AC и BD. Точка N также находится на прямой BD, поэтому мы можем использовать вторую теорему параллельных прямых для применения к точке N:

AC / CD = AN / ND.

Известно, что AC = 2y и CD = 2x-30. Подставим эти значения:

2y / (2x-30) = AN / ND.

Так как точка N является точкой пересечения, то AN и ND являются сегментами на прямой BD. Давайте обозначим отрезок AN как a и отрезок ND как b. Тогда у нас будет уравнение:

2y / (2x-30) = a / b.

Мы можем также заметить, что углы NDA и BCD являются альтернированными углами, так как BD || AC, и они равны. Таким образом, альтернированный угол NDA равен 110 градусам.

Теперь мы можем применить вторую теорему параллельных прямых для применения к точке N:

CD / BC = ND / DA.

Известно, что CD = 2x-30, BC = x-20, ND = b и DA = a. Подставим эти значения:

(2x-30) / (x-20) = b / a.

Теперь у нас есть два уравнения:

2y / (2x-30) = a / b (1)
(2x-30) / (x-20) = b / a (2)

Умножим уравнение (1) на уравнение (2):

(2y / (2x-30)) * ((2x-30) / (x-20)) = (a / b) * (b / a).

У вас может возникнуть вопрос, почему мы умножаем два уравнения. При решении системы уравнений иногда использование метода "умножить" может помочь устранить некоторые переменные и упростить вычисления.

Упростим это уравнение:

2y / (x-20) = 1.

Перенесем 2y на левую сторону уравнения:

2y = x - 20.

Далее, разделим обе стороны уравнения на 2:

y = (x - 20) / 2.

Теперь мы нашли значение переменной y.

Итак, ответ нашей задачи: x = 100 и y = (x - 20) / 2.

Я надеюсь, что объяснение было понятным и что вы легко справились с решением этой задачи. Если у вас возникли еще вопросы, не стесняйтесь задавать их.