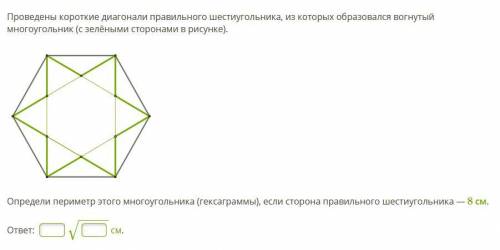
Проведены короткие диагонали правильного шестиугольника, из которых образовался вогнутый многоугольник (с зелёными сторонами в рисунке). Определи периметр этого многоугольника (гексаграммы), если сторона правильного шестиугольника — 8 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Напишите анализ эпизода из ревизор 4 действие, с 1-7 явления...
2 - Какой период и образ передает песни Эстелик Т.Казакова...
1 - Определи род выделенных глаголов холодно зима под продуло женский...
3 - Оқушы анасымен сабақ оқыды.сөйлем мүшесіне талдау...
1 - 1) 8 + ;4) 124 - 5 :52) 33+ 2 ;196. Выполните действия:+ х =...
1 - НАПИШИТЕ ПОХОЖИЙ ТЕКС ПРО ОДИН КЛУБ НО ТОКО ЧТОБ ОН БЫЛ НЕ КАК...
3 - Как определить минуты из 28°...
2 - Faxrlanmoq, anglamoq, sanamoq, ko paymoq, tortishmoq. Gap tuzish...
1 - По биологии надо составить кроссворд на тему среды жизни планеты...
2 - 1. The letter ( to write). 2. I ( to give) a very interesting...
3
2. Треугольник AKF равнобедренный AK=FK, ∡KAM=∡KFM=30°;∡AKF=120°
3. Проведём в нём перпендикуляр KM к основанию и из прямоугольного треугольника вычислим AK:
AK=AMcos30°=162:3√2=163√=163√3
4. Периметр гексаграммы состоит из 12 таких сторон:
12⋅AK=12⋅16⋅3√3=4⋅163√=643√ см
Давайте рассмотрим данную задачу пошагово:
Шаг 1: Найдем длины всех сторон в многоугольнике.
По условию, сторона правильного шестиугольника равна 8 см.
На рисунке видно, что в многоугольнике одна сторона совпадает с стороной шестиугольника. Эта сторона равна 8 см.
Также на рисунке видно, что развернутый угол в многоугольнике (шестиугольнике) составляет 180°. Значит, в вогнутом многоугольнике (гексаграммы) углы между сторонами равны 360° - 180° = 180°. Таким образом, многоугольник является правильным.
Шаг 2: Найдем длины диагоналей в многоугольнике.
На рисунке обозначены две диагонали многоугольника, образованные короткими диагоналями правильного шестиугольника.
Поскольку многоугольник является правильным, то длина каждой из этих диагоналей равна стороне шестиугольника. То есть, длина каждой диагонали равна 8 см.
Так как в многоугольнике присутствуют две диагонали, то мы имеем две диагонали длиной 8 см каждая.
Шаг 3: Найдем длину боковых сторон многоугольника.
Вогнутый многоугольник (гексаграммы) содержит 6 сторон.
Из рисунка и предыдущего шага мы знаем, что две из этих сторон равны 8 см (они совпадают с диагоналями, образованными короткими диагоналями правильного шестиугольника).
Остается 6 - 2 = 4 стороны, о которых мы не знаем ничего.
Шаг 4: Найдем длины боковых сторон многоугольника.
Поскольку многоугольник является правильным, то длина каждой из его сторон равна другой.
Таким образом, каждая из 4 оставшихся сторон равна длине всех других сторон.
Обозначим длину каждой такой стороны за "х".
Следовательно, у нас есть уравнение: 4x = 8.
Делим обе части уравнения на 4: x = 8 / 4 = 2.
Получаем, что каждая из 4 оставшихся сторон равна 2 см.
Шаг 5: Сложим длины всех сторон, чтобы найти периметр многоугольника.
Периметр многоугольника равен сумме длин всех его сторон.
Вычислим сумму: 8 + 8 + 2 + 2 + 2 + 2 = 24.
Ответ: периметр вогнутого многоугольника (гексаграммы), образованного короткими диагоналями правильного шестиугольника, равен 24 см.