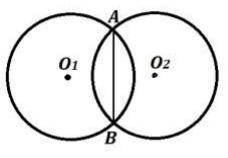
( ) Про окружности на рисунке (прикреплено) известно, что они имеют равные радиусы. Докажите, что отрезок, соединяющий центры окружностей, делит AB пополам.

Чтобы доказать, что отрезок, соединяющий центры окружностей, делит отрезок AB пополам, нам нужно использовать различные свойства окружностей и вспомогательные геометрические фигуры.

Давайте обозначим центры окружностей как O1 и O2, а отрезок, соединяющий их, как OO1O2. Также обозначим точку пересечения отрезка AB с отрезком OO1O2 как M.

Шаг 1: Рассмотрим треугольник O1AB и треугольник O2AB. Из условия задачи следует, что радиусы этих окружностей одинаковые, поэтому они равны. Таким образом, отрезки O1A и O2A равны, так как они являются радиусами окружностей.

Шаг 2: Также по условию задачи, радиусы окружностей равны, значит отрезки O1B и O2B тоже равны.

Шаг 3: Сложим равенства из шагов 1 и 2:
O1A + O1B = O2A + O2B

Шаг 4: Заметим, что отрезок AB можно разбить на две равные части следующим образом: AM и MB.

Шаг 5: Пусть точка N - середина AB. Заметим, что треугольник O1NM и треугольник O2NM являются прямоугольными треугольниками, так как NM - это серединный перпендикуляр к AB.

Шаг 6: Обозначим длину отрезка AM как x. Тогда длина отрезка BM тоже равна x.

Шаг 7: Рассмотрим треугольник O1NM. Мы знаем, что O1A равно O1B (из шага 1), а NM - это серединный перпендикуляр к AB. То есть ON является высотой этого треугольника.

Шаг 8: Так как треугольник O1NM является прямоугольным треугольником, то ON является медианой, делящей гипотенузу пополам. Значит, ON равно половине O1A.

Шаг 9: Аналогично, рассмотрим треугольник O2NM. Он также является прямоугольным треугольником и ON равно половине O2A.

Шаг 10: Зная, что радиусы окружностей равны, podemos concluir que O1A = O1B = O2A = O2B, то есть ON también es la mitad de O1B y O2B.

Шаг 11: Теперь мы можем получить, что MN = NM = x/2, так как ON делит AB пополам.

Шаг 12: Так как MN = NM = x/2, и AM = BM = x, мы можем заключить, что M - середина отрезка AB.

Таким образом, мы доказали, что отрезок, соединяющий центры окружностей, делит отрезок AB пополам.