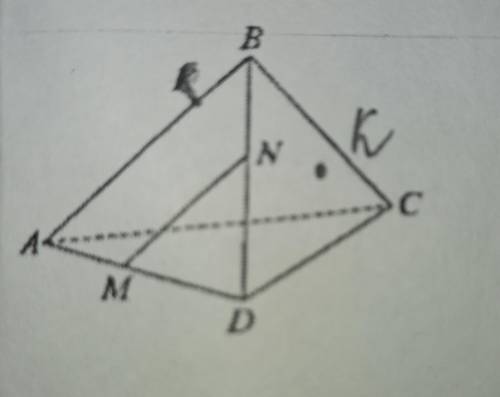
Построить сечение тетраэдра плоскость, проходящей через прямую MN и точку K, зная, что MN || AB, точка K принадлежит плоскости ABC

Для того чтобы построить сечение тетраэдра плоскостью, проходящей через прямую MN и точку K, зная что MN || AB, точка K принадлежит плоскости ABC, следуйте следующим шагам:

1. Возьмите лист бумаги и нарисуйте оси координат.
2. На выделенном участке листа нарисуйте прямую MN, параллельную прямой AB. Обозначьте точки M и N на этой прямой.
3. Обозначьте точку K на листе бумаги. Она должна находиться в плоскости ABC.
4. Найдите точку P, пересечение прямой MN и точки K. Для этого проведите прямую через точки M и K, параллельную прямой BC. Эта прямая пересечет прямую MN в точке P.
5. Проведите прямую через точки K и P. Обозначьте точку пересечения этой прямой с прямой BC как точку Q.
6. Теперь, прямая PQ представляет собой сечение тетраэдра выбранной плоскостью.

Объяснение:
MN || AB означает, что прямая MN параллельна прямой AB. Таким образом, мы можем использовать эту информацию для построения плоскости, которая проходит через прямую MN и точку K.

Точка K принадлежит плоскости ABC, что означает, что она лежит на плоскости ABC. Поэтому мы можем использовать ее положение для определения точки пересечения прямой MN с плоскостью ABC.

Чтобы определить точку пересечения прямой MN с плоскостью ABC, мы проводим прямую через точки M и K, параллельную прямой BC. Поскольку MN || AB и BC является одной из сторон тетраэдра ABCD, прямая, проходящая через точки M и K, также будет параллельна прямой BC. Эта прямая пересекает прямую MN в точке P.

Затем мы проводим прямую через точки K и P и находим точку пересечения этой прямой с прямой BC, которую мы обозначаем как точку Q. Подобным образом мы определяем все остальные точки сечения плоскости с ребрами тетраэдра.

Таким образом, плоскость, проходящая через прямую MN и точку K и параллельная прямой AB, будет представлять собой плоское сечение тетраэдра.