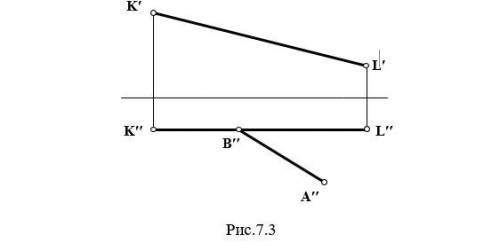
по начертательной геометрии, никак не могу решить задачу. Построить эпюр прямоугольного треугольника АВС, катеты которого равны между собой и катет ВС лежит на прямой КL (Рис. 7.3)
Другие вопросы по теме Геометрия
Популярные вопросы
- Д іть інформати в тімс умаляю...
1 - Найди наибольшее натуральное значение y, при котором верно неравенство....
3 - Перепишите предложения, в словах с орфограммой –ы/-и после приставок обозначьте...
3 - .Патріотизм, повага до батьків, вірність у дружбі й коханні- загальнолюдські...
1 - На меридіані 180° щойно розпочався новий день 26 жовтня місцевий час міст...
3 - Наблюдать за птицами. Это какое значение предлогов а) Пространственные б)...
2 - Ещё раз внимательно рассмотрите фотографию памятника С. А. Есенину. Отпишите...
2 - Диагонали равнобедренной трапеции ABCD перпендикулярны, а высота равна 7...
1 - Чи відповідають ліст і фіхте за злочини гітлера?...
1 - Зробіть конкспект :рослина - живий організм которые есть....
2
Эпюр - это плоское изображение пространственной фигуры или построение, отображающее геометрическую форму объекта. В данном случае, нам нужно построить эпюр прямоугольного треугольника АВС, где катеты АВ и АС равны между собой, а катет ВС лежит на прямой КL.
Для решения этой задачи, нам понадобятся следующие инструменты:
1. Циркуль - для построения окружностей.
2. Линейка - для измерения и построения отрезков.
3. Карандаш - для выполнения построений.
Теперь, приступим к решению задачи:
Шаг 1:
Нарисуем прямую KL, на которой будет лежать катет ВС.
Шаг 2:
Определим точку А на прямой KL.
Шаг 3:
С помощью циркуля из точки А поставим радиус, равный длине катета АВ, и построим дугу.
Шаг 4:
Отложим равный радиус от точки А и поставим вторую точку - В.
Шаг 5:
С помощью циркуля из точки В поставим радиус, равный длине катета ВС, и построим дугу, пересекающую прямую KL.
Шаг 6:
Обозначим точку пересечения второй дуги и прямой KL как С.
Шаг 7:
Проведем отрезки AB и AC, чтобы получить прямоугольный треугольник.
Шаг 8:
Теперь, когда у нас есть прямоугольный треугольник АВС, мы можем нарисовать его эпюр. Эпюр - это плоская проекция этого треугольника (т.е. плоская фигура, которая изображает геометрическую форму треугольника).
Шаг 9:
Проведем перпендикуляры из точек А, В и С на вертикальную прямую, чтобы получить проекции этих точек.
Шаг 10:
Соединим полученные точки проекций прямыми линиями. Полученная фигура будет эпюром прямоугольного треугольника АВС.
Таким образом, мы успешно построили эпюр прямоугольного треугольника АВС.