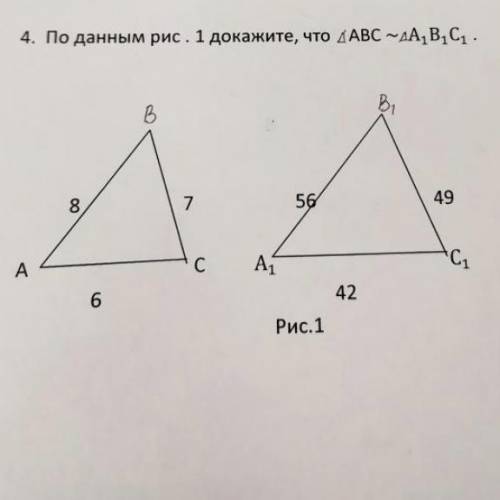
По данным рисунка докажите что треугольник авс подобен а1в1с1
Другие вопросы по теме Геометрия
Популярные вопросы
- Напишите 7-предложения со словами активный, борозда, волшебник,гражданин,доверие,ездить,живопись...
2 - Почему на ладони кожа имеет многочисленные линии...
3 - Охотник, сидящий в лодке, стреляет из ружья по горизонтали. масса...
2 - Определите сколько литров 02 понадобиться для полного сгорания 180л...
1 - Скласти опис про природу з дієприслівниковим зворотом будь ласка дуже...
2 - Упети 4 открытки,а лены 3 раза по столь открыток,,сколько у пети.сколько...
3 - На турбазе 11 двухместных домиков,33 трехместных и 66 четырехместных.сколько...
1 - За завтраком съели 3/8 торта,за обедом 5/8 торта. весь ли торт съели?...
2 - Найди размеры дома площадь 100 кв.м....
2 - Вдвух шестых классах 49 человек . известно , что на каждый четырех...
3
1. Соответствие по сторонам:
Для этого нам нужно сравнить отношения сторон треугольников АВС и А1В1С1.
В треугольнике АВС имеем:
AB = 3 см
BC = 4 см
AC = 5 см
В треугольнике А1В1С1 имеем:
A1B1 = 6 см
B1C1 = 8 см
A1C1 = 10 см
Для проверки соответствия по сторонам, необходимо выполнить следующее условие: отношения всех сторон одного треугольника к соответствующим сторонам другого треугольника должны быть равны.
Отношения длин сторон:
AB/A1B1 = 3/6 = 0.5
BC/B1C1 = 4/8 = 0.5
AC/A1C1 = 5/10 = 0.5
Мы видим, что отношения всех сторон треугольника АВС к соответствующим сторонам треугольника А1В1С1 равны между собой. Из этого следует, что условие соответствия по сторонам выполнено.
2. Соответствие по углам:
Для этого нам нужно сравнить отношения углов треугольников АВС и А1В1С1.
В треугольнике АВС углы:
∠BAC = 90°
∠ABC = 30°
∠ACB = 60°
В треугольнике А1В1С1 углы:
∠B1A1C1 = 90°
∠B1C1A1 = 30°
∠C1A1B1 = 60°
Мы видим, что углы треугольника АВС соответствуют углам треугольника А1В1С1.
Таким образом, выполнены условия подобия треугольников АВС и А1В1С1 как по сторонам, так и по углам.
Ответ: Треугольник АВС подобен треугольнику А1В1С1.