1. Геометрия
  2. Площадь треугольника abc равна

Площадь треугольника abc равна 100.de-средняя линия ,паралелльная стороне ab.найдите площадь треугольника сde

Малая1806 Малая1806    2   16.06.2019 03:30    0

Ответы
katy1231231233 katy1231231233  12.07.2020 23:57

DE - средняя линия, DE || AB. Так как у треугольников DEC и ABC угол С - общий и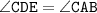 \tt \angle CDE=\angle CAB как соответственные углы, то треугольники DEC и ABC подобны по двум углам.

Средняя линия треугольника равна половине длины параллельной стороны.

DE = AB/2 , значит коэффициент подобия k=1/2.

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия, то есть

\tt \dfrac{S_{CDE}}{S_{ABC}}=k^2~~~\Rightarrow~~ S_{CDE}=k^2\cdot S_{ABC}=\dfrac{1}{4} \cdot100=25 кв. ед.


ответ: 25 кв. ед..


Площадь треугольника abc равна 100.de-средняя линия ,паралелльная стороне ab.найдите площадь треугол
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Tapty Tapty  03.08.2019 01:40
Найдите площадь а) параллелограмма, б) треугольника по двум сторонам и углу между ними: 2) а = 4 м b = √3 α = 60° 3) а = 1,7 см b = 2,2 см α = 45° 4) а = м b = м α = 30°...
anx2003 anx2003  03.08.2019 01:40
Впрямоугольной трапеции 1 боковая сторона равна 15 см а вторая 17 см. известно что меньшее основание в 2 раза меньше большого. найти площадь трапеции...
werttyu890 werttyu890  09.03.2019 10:00
Найти объём правильной треугольной пирамиды,если сторона её основания равна а,а боковое ребро образует с плоскостью основания угол в!...
TheVladChannel TheVladChannel  09.03.2019 10:00
Решить 3 по : 1. равносторонний треугольник авс вписан в окружность радиуса 6 см. найти сторону этого треугольника. 2. прямоугольный треугольник вписан в окружность радиуса 6,5 см....
7775553331 7775553331  09.03.2019 10:00
1. найдите площадь ромба, один из углов которого равен 120 градусам, а сторона 10 см. 2. в треугольнике klm, kl=2, lm=3, km=4. найдите cos k. 3. периметр параллелограмма abcd равен...
всёокок всёокок  09.03.2019 10:00
Найдите площадь параллелограмма kmno, если его большая сторона равна 4√2 см, диагональ mo равна 5 см, а угол mko равен 45°...
ник4410 ник4410  09.03.2019 10:00
Высота вк, проведенная к стороне ад параллелограмма авсд делит эту сторону на два отрезка ак = 7 см, кд = 15 см. найдите площадь параллелограмма, если...
АлинькийЦветочок5 АлинькийЦветочок5  09.03.2019 10:00
Равнобедренный треугольник авс с основанием вс вписан в окружность с центром в точке о. площадь треугольника авс, угол а = 45 град.,прямая, проходящая через точку о и середину отрезка...
lolii0ikolik lolii0ikolik  09.03.2019 10:00
Найти площадь треугольника со сторонами 8 10 7 ( само решение)...
3Таня22811 3Таня22811  09.03.2019 10:00
Найти площадь треугольника со сторонами 7,8,10...

Популярные вопросы