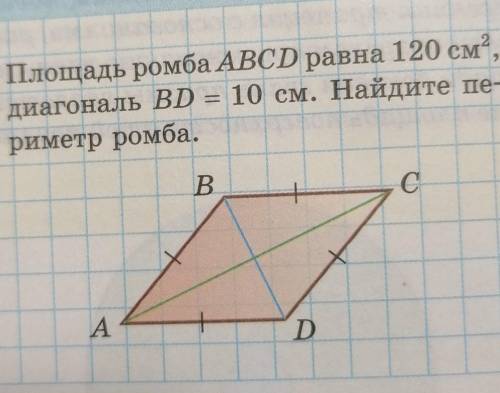
Площадь ромба ABCD равна 120см2 ,
диагональ BD = 10 см. Найдите пе-
риметр ромба.
​

Площадь ромба равна произведению его диагоналей, тогда можно записать:

S = BD* AC => AC = S : BD = 120 : 10 =12

Обозначим точку пересечения диагоналей как О.

Рассмотрим прямоугольный треугольник ABO:

Катеты являются половинами диагоналей (из св-в ромба):

BO = BD : 2= 5

AO = AC : 2 = 6

Найдем гипотенузу АВ прямоугольного треугольника ABO:

AB = √(AO²+BO²) = √(25+36)=√61

Стороны ромба равны, поэтому периметр есть

P = 4√61

Объяснение: