Площадь поверхности шара равна 20 . на расстоянии 3/2корня из pi от центра шара проведена плоскость . найти площадь полученного сечения

ответ:   2,75

Объяснение:

Площадь поверхности шара:

S = 4πR² = 20

R² = 20 / (4π) = 5/π

R = √(5/π)

О - центр шара.

OA = R = √(5/π)

С - центр сечения (круга). отрезок, соединяющий центр шара с центром сечения, перпендикулярен плоскости сечения. Значит

ОС = 3/(2√π) - расстояние от центра шара до плоскости сечения.

ΔАОС:  ∠АСО = 90°, по теореме Пифагора

            АС = √(ОА² - ОС²) =

                  =

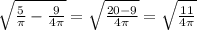
Площадь сечения:

S = π · AC²