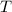Площадь полной поверхности правильной четырехугольной призмы равна t ,площадь боковой повепхности равна g. выразите сторону оснрвания призмы через t и g ответ должен быть t -g /2 под корнем
Популярные вопросы
- Сопоставьте точки зрения декабристов и правительства александра i на ключевые вопросы...
3 - Пазбор предложения: белые журавли, тихонько окликивают друг-друга, осторожное грациозно...
2 - Все изомеры до c6 алкадиенов (=,=) с3-c6 и все названия изомеров...
3 - Время до поступления первой заявки в систему массового обслуживания имеет показательное...
3 - Одноатомный спирт, содержит 34,79 кислорода 13,04 водорода и углерод. определите...
1 - Продолжи ряды однородных членов предложения на какой вопрос они отвечают какому...
3 - Уічній прогресії знайдіть а1 і b, якщо а3=-80, а8=-25...
2 - Подскажите , автора этого учебника по 7 класс...
3 - Из одного города в противоположных направлениях одновременно отправились два автомобиля...
1 - Нужно, решите хотя бы пару , свои последнии , огромное вам...
1
Объяснение:
Пусть - сторона основания этой призмы, тогда
- сторона основания этой призмы, тогда 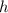 - высота этой призмы.
- высота этой призмы.
S полн. поверх. = 2S осн. + S бок. поверх. = 2a² + P осн. * h =