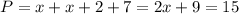с геометрией найти периметр через теорему косинусов
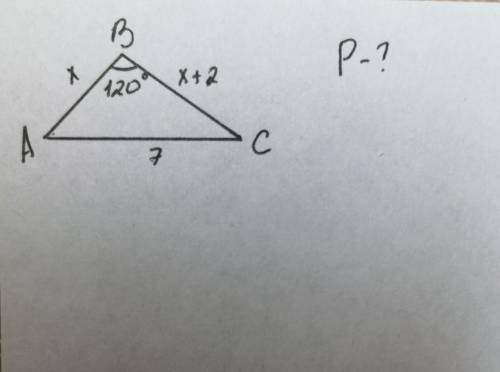
Другие вопросы по теме Геометрия
Популярные вопросы
- Поясните,какие эритроциты( человека или лягушки) переносят больше...
2 - Школний спортивний майданчык прямоугольной форми займайет 300 м²....
3 - прочитайте фрагмент стихотворения казахстанского автора п. васильева...
2 - 1целая 1/3 в 4 степени . решите...
3 - Написан ли этот текст в публицистическом стиле? какой жанр? и придумаете...
2 - 72 () ссора на перемене - составить 5 диалогов (текстов) разных...
1 - Обьем газа при нормальных условиях равен 15,6 л. найдите его обьем...
2 - На круги эйлера! нужен в группе 43 студента: 25 студентов посещает...
1 - Разжелите на три столбика в первый столбик инфинитив во второй паст...
3 - Завтра у меня контрольная. большое. 7 класс...
2
15
Объяснение:
По теореме косинусов
Получаем квадратное уравнение
По теореме Виета корни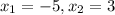
Подходит только
Тогда периметр