Площадь полной поверхности правильного тетраэдра составляет 120 корней из 3 см^2. найдите его высоту.
Ответы
Если ребро тетраэдра равна  , высота правильного тетраэдра проецируется в центр описанной окружности описанной около правильного треугольника на которую опущена высота
, высота правильного тетраэдра проецируется в центр описанной окружности описанной около правильного треугольника на которую опущена высота 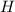 , а радиус описанной окружности равен
, а радиус описанной окружности равен
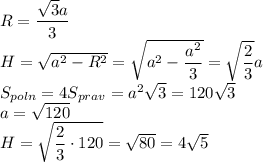
ПОКАЗАТЬ ОТВЕТЫ
 , высота правильного тетраэдра проецируется в центр описанной окружности описанной около правильного треугольника на которую опущена высота
, высота правильного тетраэдра проецируется в центр описанной окружности описанной около правильного треугольника на которую опущена высота 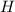 , а радиус описанной окружности равен
, а радиус описанной окружности равен 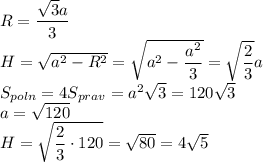
Другие вопросы по теме Геометрия
Популярные вопросы
- Балшыктын катуы, агашты жаруы, судын катуы кайсыга жатады? физикалық...
2 - Выпишите эпитеты, которыми автор характерезует Энеи. О чём говорит?...
2 - Спишите предложения из произведений А. П. Чехова, расставляя запятые....
3 - поомгите класс сор все подробно (все действия и тд)расписать желательно...
1 - Предложите меры по предотвращению последствий атмосферной засухи...
1 - При свободном падении тело проходит в первую секунду 5м, а в каждую...
3 - Соотнесите стихотворные строки и размер, которым они написаны: *...
1 - Соотносимые типы вешивки с рисункамию...
2 - Найти причастия в предложении: В Сиракузах он окружен почетом вниманием...
2 - Sandy (get up), (wash) her face, (do) her morning exercises and (go)...
3